
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 354 Атанасян — Подробные Ответы
Через три данные точки проведите окружность. Всегда ли задача имеет решение?
Соедините точки A, B и C отрезками.
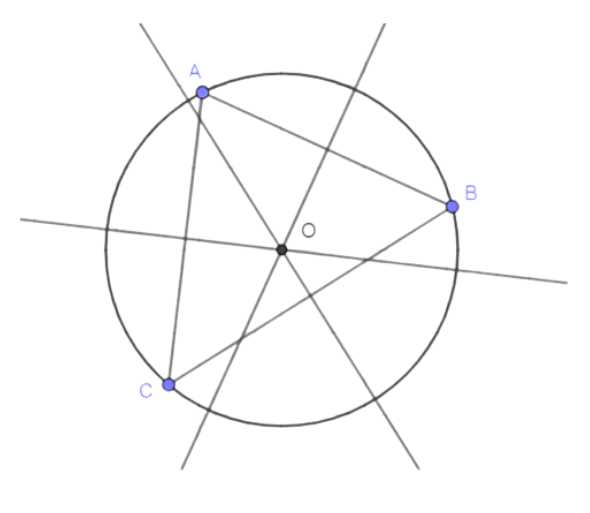
Для построения окружности, проходящей через три заданные точки A, B и C, необходимо выполнить следующие действия:
1. Соедините точки A и B отрезком AB. Также соедините точки B и C отрезком BC, а точки A и C отрезком AC. Таким образом, получатся три отрезка: AB, BC и AC.
2. Найдите середину каждого из этих отрезков. Для этого измерьте длину каждого отрезка и разделите её пополам. Обозначьте середины отрезков, например, M₁ для AB, M₂ для BC и M₃ для AC.
3. Постройте серединные перпендикуляры для каждого из отрезков. Для этого:
— Установите циркуль в точку A, радиусом сделайте больше половины длины отрезка AB, и проведите дугу.
— Повторите те же действия из точки B, чтобы дуги пересеклись. Соедините точки пересечения дуг прямой линией. Это будет серединный перпендикуляр к отрезку AB.
— Аналогично постройте серединные перпендикуляры для отрезков BC и AC.
4. Найдите точку пересечения всех трёх серединных перпендикуляров. Эта точка является центром окружности, которая проходит через точки A, B и C. Обозначьте её буквой O.
5. Измерьте расстояние от точки O до любой из точек A, B или C. Это расстояние будет радиусом окружности. Например, если вы измерили расстояние от O до A, то это расстояние обозначим как r.
6. Постройте окружность с центром в точке O и радиусом r. Для этого установите циркуль в точку O, установите радиус r и проведите окружность.
7. Проверьте, что построенная окружность проходит через все три точки A, B и C. Если окружность проходит через эти точки, то задача решена.
8. Если серединные перпендикуляры не пересекаются в одной точке, это значит, что точки A, B и C не лежат на одной окружности, и задача не имеет решения.
Таким образом, результатом будет окружность, проходящая через точки A, B и C, либо вывод о невозможности построения окружности, если точки не равноудалены друг от друга.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!