
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 353 Атанасян — Подробные Ответы
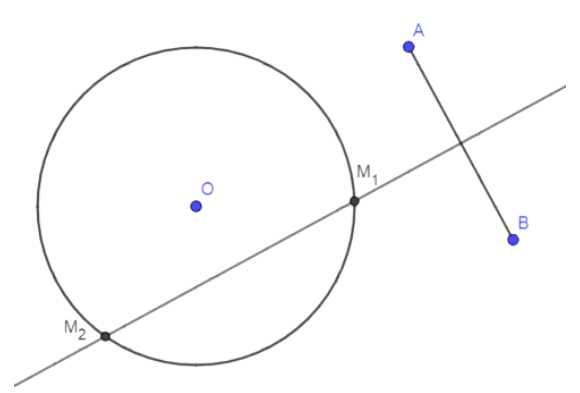
Постройте точку, лежащую на данной окружности и равноудалённую от концов данного отрезка. Сколько решений может иметь задача?
Соедините точки A и B отрезком и найдите его середину. Постройте серединный перпендикуляр к отрезку AB. Найдите точки пересечения этого перпендикуляра с заданной окружностью. Если пересечения две, то это искомые точки. Если одно, то это единственная точка. Если пересечений нет, решения не существует.
Для решения задачи выполните следующие шаги:
1. Соедините точки A и B отрезком. Это позволит определить расстояние между точками, а также найти середину данного отрезка.
2. Найдите середину отрезка AB. Для этого измерьте длину отрезка и разделите её пополам. Отметьте середину на отрезке и обозначьте её, например, буквой O₁.
3. Постройте серединный перпендикуляр к отрезку AB. Для этого проведите прямую, которая проходит через точку O₁ (середину отрезка) и перпендикулярна отрезку AB. Это можно сделать с помощью циркуля и линейки:
— Установите циркуль в точку A и нарисуйте дугу, радиус которой больше половины длины отрезка AB.
— Не меняя радиус, повторите то же самое из точки B, чтобы дуги пересеклись в двух местах.
— Соедините точки пересечения дуг прямой линией. Это и будет серединный перпендикуляр.
4. Рассмотрите окружность, данную в задаче. Определите, пересекается ли серединный перпендикуляр с окружностью. Возможны три случая:
— Если серединный перпендикуляр не пересекает окружность, то решение задачи отсутствует.
— Если серединный перпендикуляр касается окружности, то точка касания будет единственным решением.
— Если серединный перпендикуляр пересекает окружность в двух точках, то эти две точки являются решениями задачи.
5. Найдите точки пересечения серединного перпендикуляра и окружности. Для этого используйте циркуль и линейку:
— Установите циркуль в центр окружности и проведите радиус до пересечения с серединным перпендикуляром.
— Отметьте точки пересечения серединного перпендикуляра с окружностью и обозначьте их, например, M₁ и M₂.
6. Проверьте, что точки M₁ и M₂ равноудалены от точек A и B. Для этого измерьте расстояния от M₁ до A и B, а также от M₂ до A и B. Они должны быть равны.
7. Точки M₁ и M₂ являются искомыми точками, лежащими на окружности и равноудалёнными от концов отрезка AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!