ГДЗ по Геометрии 7 класс Номер 352 Атанасян — Подробные Ответы

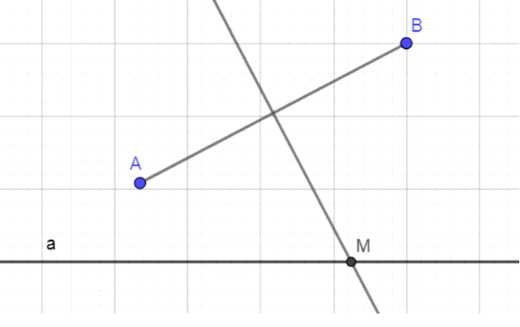
Даны две точки A и B и прямая а, не проходящая через эти точки. На прямой а постройте точку, равноудалённую от точек A и B. Всегда ли задача имеет решение?

Соединяем точки A и B отрезком. Находим середину этого отрезка и проводим через неё серединный перпендикуляр. Определяем точку пересечения серединного перпендикуляра с прямой a. Эта точка будет равноудалена от точек A и B.

Дано: необходимо построить на прямой a точку, которая будет равноудалена от двух заданных точек A и B.

Решение:

1. Соединяем точки A и B прямым отрезком AB. Это необходимо для того, чтобы определить расстояние между этими точками и построить серединный перпендикуляр.

2. Находим середину отрезка AB. Для этого измеряем длину отрезка AB и делим её пополам. Отмечаем точку посередине отрезка и обозначаем её, например, буквой O.

3. Строим серединный перпендикуляр к отрезку AB. Для этого через точку O проводим прямую, которая пересекает отрезок AB под прямым углом (90 градусов). Этот перпендикуляр будет являться геометрическим местом точек, равноудалённых от A и B.

4. Определяем точку пересечения серединного перпендикуляра с прямой a. Для этого проводим прямую a и смотрим, где она пересекается с серединным перпендикуляром. Отмечаем точку пересечения и обозначаем её буквой M.

5. Проверяем, что точка M действительно равноудалена от точек A и B. Для этого измеряем расстояния от M до A и от M до B. Если они равны, то точка M является искомой.

Если прямая a перпендикулярна отрезку AB, то задача имеет решение только в случае, если прямая a совпадает с серединным перпендикуляром. В таком случае точка M будет совпадать с серединой отрезка AB.

Ответ: точка M, найденная вышеописанным способом, является искомой точкой, равноудалённой от точек A и B.