ГДЗ по Геометрии 7 класс Номер 351 Атанасян — Подробные Ответы

Постройте треугольник по двум сторонам и высоте к третьей стороне. Решение
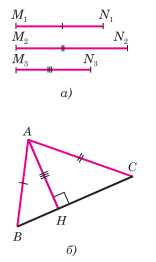
Даны три отрезка M1N1, M2N2, M3N3 (рис. 148, а). Требуется построить такой треугольник ABC, у которого две стороны, скажем AB и AC, равны соответственно данным отрезкам M1N1 и M2N2, а высота AH равна отрезку M3N3. Проведём решение задачи по описанной схеме.

Допустим, что искомый треугольник ABC построен (рис. 148, б). Мы видим, что сторона AB и высота AH являются гипотенузой и катетом прямоугольного треугольника ABH. Поэтому построение треугольника ABC можно провести по такому плану: сначала построить прямоугольный треугольник ABH, а затем достроить его до всего треугольника ABC.

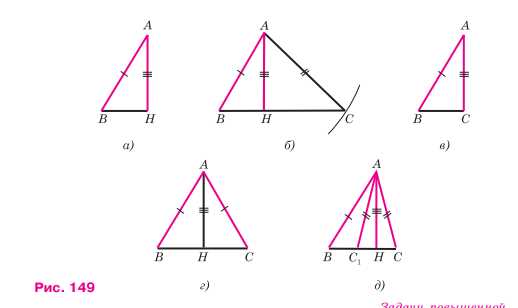
Строим прямоугольный треугольник ABH, у которого гипотенуза AB равна отрезку M1N1, а катет AH равен данному отрезку M3N3. Как это сделать, мы знаем (задача 314, в). На рисунке 149, а изображён построенный треугольник ABH. Затем проводим окружность радиуса M2N2 с центром в точке A. Одну из точек пересечения этой окружности с прямой BH обозначим буквой C. Проведя отрезки BC и AC, получим искомый треугольник ABC (рис. 149, б).

Треугольник ABC действительно искомый, так как по построению сторона AB равна M1N1, сторона AC равна M2N2, а высота AH равна M3N3, т. е. треугольник ABC удовлетворяет всем условиям задачи.

Нетрудно сообразить, что задача имеет решение не при любых данных отрезках M1N1, M2N2, M3N3. В самом деле, если хотя бы один из отрезков M1N1 и M2N2 меньше M3N3, то задача не имеет решения, так как наклонные AB и AC не могут быть меньше перпендикуляра AH. Задача не имеет решения и в том случае, когда M1N1 = M2N2 = M3N3 (объясните почему).

В остальных случаях задача имеет решение. Если M1N1 > M3N3, а M2N2 = M3N3, то задача имеет единственное решение: в этом случае сторона AC совпадает с высотой AH и искомый треугольник является прямоугольным (рис. 149, в). Если M1N1 > M3N3, а M2N2 = M1N1, то задача также имеет единственное решение: в этом случае треугольник ABC равнобедренный (рис. 149, г). И наконец, если M1N1 > M3N3, M2N2 > M3N3 и M1N1 ≠ M2N2, то задача имеет два решения — треугольники ABC и ABC1 на рисунке 149, д.

Даны три отрезка: две стороны и высота к третьей стороне.

Построение: 1. Постройте прямоугольный треугольник ABH, где AB – гипотенуза, равная первой стороне, а AH – катет, равный высоте. 2. Проведите окружность с центром в точке A и радиусом, равным второй стороне. 3. Найдите точку пересечения окружности с прямой BH и обозначьте её как C. 4. Соедините точки AC и BC, получив искомый треугольник.

Задача имеет решение, если высота меньше обеих сторон. В некоторых случаях возможно одно или два решения.

Даны три отрезка: M1N1, M2N2 и M3N3. Требуется построить треугольник ABC, у которого две стороны равны M1N1 и M2N2, а высота к третьей стороне равна M3N3.

Решение:

1. Построим прямоугольный треугольник ABH, где AB – гипотенуза, равная отрезку M1N1, а AH – катет, равный отрезку M3N3.
Для этого:
а) Проведите отрезок AB длиной M1N1.
б) Из точки A проведите перпендикуляр AH к AB длиной M3N3.

2. На основе построенного треугольника ABH достраиваем треугольник ABC.
а) Из точки A проведите окружность радиусом, равным отрезку M2N2.
б) Найдите точку пересечения этой окружности с прямой BH. Полученные точки пересечения обозначьте как C и C1.

3. Соедините точки AC и BC. Полученные треугольники ABC и ABC1 являются решениями задачи.

Доказательство:
Стороны AB и AC равны заданным отрезкам M1N1 и M2N2 соответственно, а высота AH равна M3N3. Следовательно, построенный треугольник соответствует условиям задачи.

Исследование:
Задача имеет решение только при выполнении следующих условий:
а) Высота M3N3 должна быть меньше каждой из сторон M1N1 и M2N2, так как наклонные не могут быть меньше перпендикуляра.
б) Если одна из сторон равна высоте, то треугольник будет прямоугольным.
в) Если обе стороны равны, то треугольник будет равнобедренным.
г) В общем случае, если M1N1 > M3N3 и M2N2 > M3N3, задача может иметь два решения (два треугольника).

Итог: Построение завершено, треугольник найден.