ГДЗ по Геометрии 7 класс Номер 349 Атанасян — Подробные Ответы

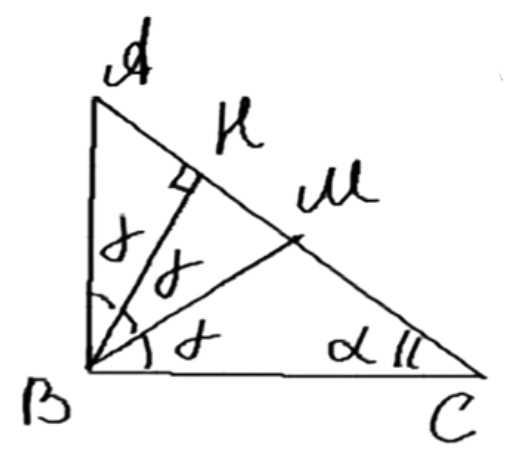
Медиана и высота треугольника, проведённые из одной вершины угла треугольника, делят этот угол на три равные части. Докажите, что треугольник прямоугольный.

Дано: треугольник ABC, CM — медиана, CH — высота. Требуется доказать, что треугольник ABC прямоугольный.

Рассмотрим треугольник ACM. Так как CH — высота и медиана, то треугольник ACM равнобедренный, и углы ∠ACH и ∠MCH равны. Пусть они равны α. Также MB = 2HM, где HM = AH.

Треугольники CHM и CDM равны по гипотенузе CM и углу α. Следовательно, NH = MD. В прямоугольном треугольнике MDB отрезок MD равен половине MB, значит угол ∠B равен 30°.

В треугольнике BCH угол ∠BCH равен 90° — ∠B = 60°. Так как ∠BCH = 2α, то 2α = 60°, откуда α = 30°. Угол ∠C равен 3α = 90°.

Следовательно, треугольник ABC прямоугольный.

Дано: треугольник ABC, CM — медиана, CH — высота. Требуется доказать, что треугольник ABC прямоугольный.

Рассмотрим решение.

1. Пусть углы ∠ACH, ∠MCH и ∠MCB равны α. Это следует из того, что CH — высота и медиана треугольника ACM, а также из равенства углов при основании равнобедренного треугольника ACM.

2. Так как CH одновременно является высотой и медианой треугольника ACM, то треугольник ACM равнобедренный. Следовательно, отрезки AH и HM равны, то есть AH = HM = x. Кроме того, MB равен удвоенной длине HM, поэтому MB = 2x.

3. Проведем прямую MD, перпендикулярную стороне BC. Это позволяет нам рассмотреть дополнительные прямоугольные треугольники.

4. Рассмотрим прямоугольные треугольники CHM и CDM. У них общая гипотенуза CM, а углы ∠MCH и ∠MCB равны по условию (они равны α). Следовательно, треугольники CHM и CDM равны по гипотенузе и острому углу. Из равенства треугольников следует, что отрезки NH и MD равны, то есть NH = MD = x.

5. Теперь рассмотрим прямоугольный треугольник MDB. В этом треугольнике MD составляет половину MB, то есть MD = 1/2 MB. Так как MB = 2x, то MD = x. Угол ∠B в треугольнике MDB равен 30°, так как противолежащий катет MD равен половине гипотенузы MB.

6. Рассмотрим прямоугольный треугольник BCH. Угол ∠BCH равен разности между прямым углом и углом ∠B, то есть ∠BCH = 90° — ∠B. Подставляя значение ∠B = 30°, получаем ∠BCH = 90° — 30° = 60°.

7. Угол ∠BCH равен 2α (по условию задачи и равенству углов). Следовательно, 2α = 60°, откуда α = 30°.

8. Угол ∠C в треугольнике ABC равен сумме углов ∠ACH, ∠MCH и ∠MCB, то есть ∠C = α + α + α = 3α. Подставляя значение α = 30°, получаем ∠C = 3 × 30° = 90°.

Таким образом, угол ∠C равен 90°, что доказывает, что треугольник ABC является прямоугольным. Это и требовалось доказать.