
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 347 Атанасян — Подробные Ответы
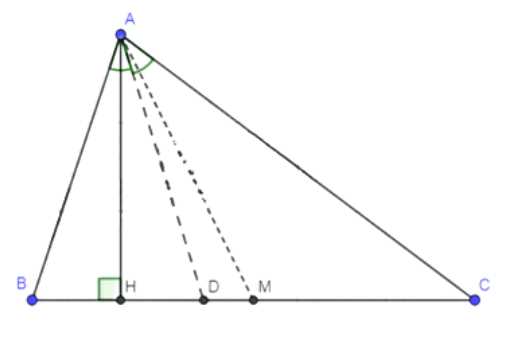
Докажите, что в неравнобедренном треугольнике основание биссектрисы треугольника лежит между основаниями медианы и высоты, проведённых из этой же вершины.
Дано: треугольник ABC, где AM — медиана, AD — биссектриса, AH — высота. Требуется доказать, что D лежит на HM.
Пусть AB < AC. Тогда угол ADB < угла ADC, так как напротив меньшей стороны лежит меньший угол. Углы ADB и ADC смежные, их сумма равна 180 градусов. Следовательно, угол ADB < 90 градусов, а угол ADC > 90 градусов. Так как угол ADC тупой, высота AH пересекает продолжение стороны DC, то есть точка H лежит на продолжении DC. Поскольку медиана AM делит сторону BC на равные части, а AB < AC, то BD < CD. Таким образом, точка D находится на отрезке BC ближе к B, а точка H лежит на продолжении DC. Это означает, что D лежит на HM, что и требовалось доказать.
Дано: треугольник ABC, где AM — медиана, AD — биссектриса, AH — высота. Необходимо доказать, что точка D лежит на отрезке HM.
1. Рассмотрим стороны треугольника ABC. Пусть AB < AC. По свойству треугольника напротив меньшей стороны лежит меньший угол. Это означает, что угол ADB меньше угла ADC. То есть ADB < ADC.
2. Углы ADB и ADC являются смежными, так как AD — биссектриса, делящая угол BAC на две равные части. Сумма смежных углов равна 180 градусам. Следовательно, ADB + ADC = 180 градусов. Из этого следует, что угол ADB острый (меньше 90 градусов), а угол ADC тупой (больше 90 градусов).
3. Рассмотрим треугольник ADC. Поскольку угол ADC тупой, высота AH, проведенная из вершины A, пересекает сторону BC или её продолжение. Это значит, что точка H находится либо на отрезке BC, либо на его продолжении. Однако, учитывая, что угол ADC больше 90 градусов, точка H обязательно лежит на продолжении стороны DC.
4. По свойству медианы AM, точка M делит сторону BC на две равные части. Это означает, что BM = MC. Так как AB < AC, то BD < CD. Следовательно, точка D, которая является серединой стороны BC, ближе к точке B, чем к точке C.
5. Теперь рассмотрим расположение точек H и D. Поскольку H лежит на продолжении стороны DC, а D находится на стороне BC, то отрезок HM соединяет эти две
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!