
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 343 Атанасян — Подробные Ответы
Две стороны треугольника не равны друг другу. Докажите, что медиана, проведённая из их общей вершины, составляет с меньшей из сторон больший угол.
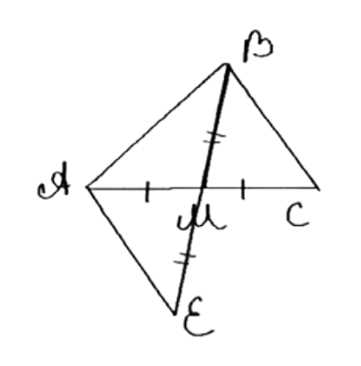
Дано: треугольник ABC, BM — медиана, AB > BC. Требуется доказать, что угол CBM больше угла ABM.
На продолжении BM отметим точку E так, чтобы ME = BM. Рассмотрим треугольники ABM и CEM. В них ME = BM по построению, AM = MC так как BM — медиана, углы AMB и EMC равны как вертикальные. Следовательно, треугольники ABM и CEM равны. Из этого следует, что AB = CE и угол ABM равен углу MEC. Так как AB > BC и CE = AB, то BC > CE. В треугольнике BCE угол MBC меньше угла BEC, так как BC > CE. Угол BEC равен углу ABM, значит угол CBM больше угла ABM. Доказано.
Дано: треугольник ABC, где BM — медиана, AB > BC. Требуется доказать, что угол CBM больше угла ABM.
Решение:
1. На продолжении отрезка BM отметим точку E так, чтобы ME = BM. Это построение позволит использовать свойства равных отрезков в дальнейших рассуждениях.
2. Рассмотрим треугольники ABM и CEM. В этих треугольниках:
— ME = BM (по построению),
— AM = MC (так как BM — медиана, следовательно, точка M делит сторону AC пополам),
— угол AMB равен углу EMC (как вертикальные углы).
По признаку равенства треугольников (две стороны и угол между ними) треугольники ABM и CEM равны.
3. Из равенства треугольников ABM и CEM следует, что AB = CE и угол ABM равен углу MEC.
4. Так как по условию AB > BC, а из предыдущего шага известно, что CE = AB, то можно утверждать, что BC > CE.
5. Рассмотрим треугольник BCE. В этом треугольнике угол MBC лежит против стороны CE, а угол BEC лежит против стороны BC. Так как BC > CE (вывод из шага 4), то угол BEC больше угла MBC.
6. Учитывая, что угол BEC равен углу ABM (следствие равенства треугольников ABM и CEM), получаем, что угол ABM больше угла MBC.
7. Таким образом, угол CBM больше угла ABM, так как угол CBM состоит из угла MBC и дополнительно угла между сторонами BC и BM.
Вывод: доказано, что угол CBM больше угла ABM.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!