ГДЗ по Геометрии 7 класс Номер 341 Атанасян — Подробные Ответы

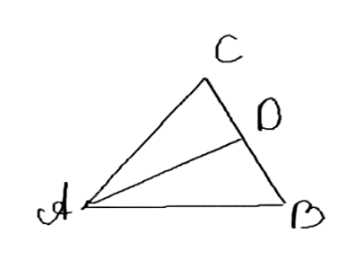
В треугольнике ABC сторона AB больше стороны АС, отрезок AD — биссектриса. Докажите, что ∠ADB > ∠ADC и BD > CD.

Дано: AB > AC, AD — биссектриса.

По свойству биссектрисы BD / AB = CD / AC, значит BD / CD = AB / AC. Так как AB > AC, то BD > CD.

Углы выразим через углы треугольника: ∠ADC = 180° — ∠CAD — ∠ACB, ∠ADB = 180° — ∠BAD — ∠ABC. Поскольку ∠CAD = ∠BAD (AD — биссектриса), а ∠ACB > ∠ABC (против большей стороны лежит больший угол), то ∠ADB > ∠ADC.

Доказано, что BD > CD и ∠ADB > ∠ADC.

Дано: в треугольнике ABC сторона AB больше стороны AC (AB > AC), AD является биссектрисой угла A. Требуется доказать два утверждения: угол ADB больше угла ADC (∠ADB > ∠ADC) и отрезок BD больше отрезка CD (BD > CD).

Рассмотрим доказательство.

1. По свойству биссектрисы известно, что она делит противоположную сторону треугольника на отрезки, пропорциональные прилежащим сторонам. Это означает, что BD / AB = CD / AC. Из этого следует, что отношение BD к CD равно отношению AB к AC: BD / CD = AB / AC.

2. Так как по условию AB > AC, то отношение BD / CD также больше единицы. Следовательно, BD > CD. Первое утверждение доказано.

3. Теперь рассмотрим углы ADB и ADC. Выразим их через углы треугольника. Для угла ADC: ∠ADC = 180° — ∠CAD — ∠ACB. Для угла ADB: ∠ADB = 180° — ∠BAD — ∠ABC.

4. Заметим, что углы ∠CAD и ∠BAD равны, так как AD — биссектриса. Кроме того, из условия AB > AC следует, что угол ∠ACB больше угла ∠ABC (по свойству треугольника, против большей стороны лежит больший угол).

5. Поскольку ∠ACB > ∠ABC, то разность углов в выражении для ∠ADC будет меньше, чем разность углов в выражении для ∠ADB. Это приводит к выводу, что ∠ADB > ∠ADC.

Таким образом, оба утверждения доказаны: BD > CD и ∠ADB > ∠ADC.