
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 340 Атанасян — Подробные Ответы
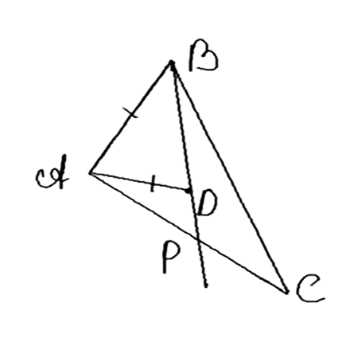
Внутри треугольника ABC взята такая точка D, что AD = AB.
Докажите, что АС > AB.
Дано: треугольник ABC, отрезок AD равен AB. Требуется доказать, что AC больше AB.
Продлим отрезок AD до пересечения с прямой BC в точке E. По построению AD меньше AE. Учитывая, что AD равно AB, следует, что AE больше AB. Согласно свойствам треугольника, одна из сторон должна быть больше другой. Так как AE меньше AC, то AC больше AB. Доказано.
Дано: треугольник ABC, отрезок AD равен AB. Требуется доказать, что AC больше AB.
Рассмотрим построение. Продлим отрезок AD до пересечения с прямой BC и обозначим точку пересечения как E. По построению очевидно, что длина отрезка AD меньше длины отрезка AE, так как точка E лежит за пределами точки D на продолжении прямой AD.
Теперь обратимся к задаче, которая утверждает, что для любого треугольника выполняется одно из следующих условий: либо AE меньше AB, либо AE меньше AC. Это утверждение можно обосновать тем, что в треугольнике длина медианы или любого другого отрезка, соединяющего вершину с противоположной стороной, всегда меньше длины самой стороны треугольника, если она не является ее продолжением.
Поскольку по условию задачи отрезок AD равен AB, а из построения следует, что AD меньше AE, то автоматически AE больше AB. Это исключает возможность того, что AE меньше AB, и остается единственный возможный случай: AE меньше AC.
Таким образом, если AE меньше AC, а AE больше AB, то из этого следует, что AC больше AB. Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!