
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 339 Атанасян — Подробные Ответы
Отрезок ВВ1 — биссектриса треугольника ABC. Докажите, что ВА > В1A и BС > В1С.
Дано треугольник ABC с биссектрисой BB1.
Угол ABB1 равен углу B1BC, так как BB1 делит угол ABC пополам. Угол BB1A равен сумме углов B1BC и BCB1, поэтому BB1A больше угла B1BC и угла ABB1. В треугольнике ABB1 угол BB1A лежит против стороны AB, а угол ABB1 против AB1. Так как BB1A больше ABB1, то AB > AB1. Угол BB1C равен сумме углов ABB1 и AB1B, поэтому BB1C больше угла B1BC. В треугольнике BCB1 угол BB1C лежит против стороны BC, а угол B1BC против B1C. Так как BB1C больше B1BC, то BC > B1C. Доказано, что AB > AB1 и BC > B1C.
Дано: треугольник ABC, биссектриса BB1.
Требуется доказать: AB > AB1 и BC > B1C.
Рассмотрим последовательное доказательство:
1. Угол ABB1 равен углу B1BC. Это следует из определения биссектрисы, так как BB1 делит угол ABC на два равных угла.
2. Угол BB1A равен сумме углов B1BC и BCB1. Это утверждение основано на свойстве внешнего угла треугольника, который равен сумме двух внутренних углов, не смежных с ним. Следовательно, угол BB1A больше угла B1BC, а также больше угла ABB1.
3. Рассмотрим треугольник ABB1. В этом треугольнике угол BB1A лежит против стороны AB, а угол ABB1 лежит против стороны AB1. Так как угол BB1A больше угла ABB1, то по свойству треугольника, против большего угла лежит большая сторона, можно сделать вывод: AB > AB1.
4. Угол BB1C равен сумме углов ABB1 и AB1B. Это также вытекает из свойства внешнего угла треугольника. Следовательно, угол BB1C больше угла ABB1, а также больше угла B1BC.
5. Рассмотрим треугольник BCB1. В этом треугольнике угол BB1C лежит против стороны BC, а угол B1BC лежит против стороны B1C. Так как угол BB1C больше угла B1BC, то по тому же свойству треугольника, против большего угла лежит большая сторона, можно заключить: BC > B1C.
Вывод: доказано, что AB > AB1 и BC > B1C.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


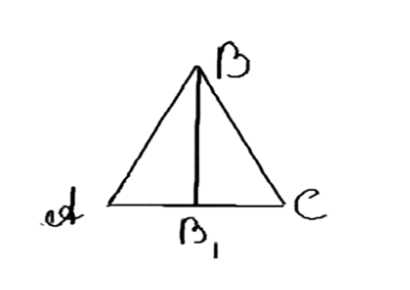

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!