
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 338 Атанасян — Подробные Ответы
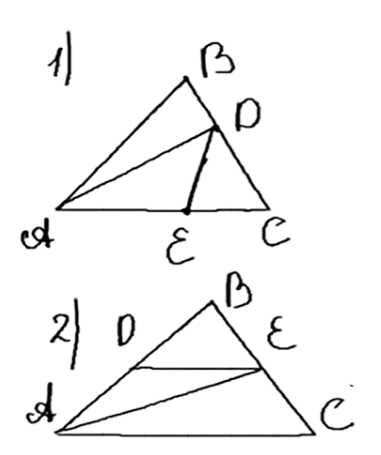
Докажите, что любой отрезок с концами на разных сторонах треугольника не больше наибольшей из сторон треугольника.
Дано треугольник ABC, где AB наибольшая сторона. Требуется доказать, что DE < AB.
Рассмотрим два случая. Первый случай: один из концов DE лежит на AB. Тогда DE ≤ AE или DE ≤ BE. Так как AE < AB и BE ≤ BC < AB, то DE < AB.
Второй случай: ни один из концов DE не лежит на AB. Тогда DE ≤ AE или DE ≤ CE. Так как AE < AB и CE ≤ BC < AB, то DE < AB.
Следовательно, во всех случаях DE < AB.
Дано: треугольник ABC, где AB является наибольшей стороной. Требуется доказать, что DE < AB.
Рассмотрим два возможных случая расположения отрезка DE.
Первый случай: один из концов отрезка DE лежит на стороне AB.
В этом случае, если отрезок соединяет вершину треугольника с точкой, лежащей на противоположной стороне, то он всегда меньше большей из двух других сторон треугольника. Это следует из свойства треугольника, что любой отрезок, соединяющий вершину с точкой на противоположной стороне, меньше самой длинной стороны. Следовательно, AE < AB.
Теперь рассмотрим треугольник ADE. Для стороны DE справедливо одно из двух неравенств: DE ≤ AE или DE ≤ BE.
Так как AE < AB (по доказанному выше), а BE ≤ BC и BC < AB (так как AB – наибольшая сторона треугольника), то из этого следует, что DE < AB.
Второй случай: ни один из концов отрезка DE не лежит на стороне AB.
В этом случае AE – это отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне. По тому же свойству треугольника, что и в первом случае, AE < AB.
Рассмотрим треугольник AEC. Для стороны DE справедливо одно из двух неравенств: DE ≤ AE или DE ≤ CE.
Поскольку AE < AB (по доказанному ранее), а CE ≤ BC и BC < AB (так как AB – наибольшая сторона треугольника), то из этого также следует, что DE < AB.
Таким образом, во всех возможных случаях расположения отрезка DE доказано, что DE < AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!