
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 334 Атанасян — Подробные Ответы
Через каждую вершину данного треугольника проведена прямая, перпендикулярная к биссектрисе треугольника, исходящей из этой вершины. Отрезки этих прямых вместе со сторонами данного треугольника образуют три треугольника. Докажите, что углы этих треугольников соответственно равны.
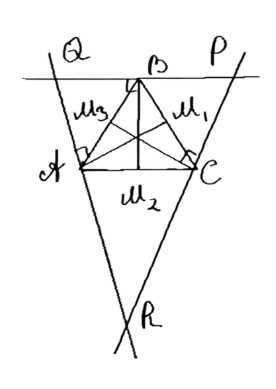
Дано: в треугольнике ABC проведены биссектрисы AM1, BM2, CM3. Прямые QR, QP, RP перпендикулярны соответственно AM1, BM2, CM3. Требуется доказать, что треугольники AQB, BPC, ARC подобны.
Рассмотрим биссектрису AM1. Она делит угол BAC пополам, поэтому угол M1AC = BAM1 = 1/2 BAC. Так как QR перпендикулярна AM1, угол CAR = 90° — 1/2 BAC. Аналогично для биссектрисы CM3 угол BCM3 = ACM3 = 1/2 BCA, а угол BCP = 90° — 1/2 BCA. Для биссектрисы BM2 угол ABM2 = M2BC = 1/2 ABC, а угол AQB = 90° — 1/2 ABC.
В треугольнике BPC угол BPC = 180° — (90° — 1/2 ABC) — (90° — 1/2 BCA) = 90° — 1/2 BAC. В треугольнике ARC угол CRA = 180° — (90° — 1/2 BAC) — (90° — 1/2 BCA) = 90° — 1/2 ABC. В треугольнике AQB угол AQB = 180° — (90° — 1/2 BAC) — (90° — 1/2 ABC) = 90° — 1/2 BCA.
Углы треугольников AQB, BPC, ARC равны: угол AQB = угол BPC = угол CRA = 90° — 1/2 BCA, угол QAB = угол PBC = угол CAR = 90° — 1/2 BAC, угол QBA = угол PCB = угол ACR = 90° — 1/2 ABC. Следовательно, треугольники подобны.
Дано: В треугольнике ABC проведены биссектрисы AM1, BM2, CM3. Прямые QR, QP, RP перпендикулярны соответственно AM1, BM2, CM3. Требуется доказать, что треугольники AQB, BPC, ARC подобны.
Решение:
1. Рассмотрим биссектрису AM1. Поскольку AM1 — это биссектриса, то она делит угол BAC пополам. Следовательно, угол M1AC равен углу BAM1 и составляет половину угла BAC, то есть M1AC = BAM1 = 1/2 BAC. Угол CAR, образованный прямой QR и стороной AC, равен 90° — 1/2 BAC, так как QR перпендикулярна AM1.
2. Аналогично рассмотрим биссектрису CM3. Поскольку CM3 — это биссектриса, то она делит угол BCA пополам. Следовательно, угол BCM3 равен углу ACM3 и составляет половину угла BCA, то есть BCM3 = ACM3 = 1/2 BCA. Угол BCP, образованный прямой RP и стороной BC, равен 90° — 1/2 BCA, так как RP перпендикулярна CM3.
3. Рассмотрим биссектрису BM2. Поскольку BM2 — это биссектриса, то она делит угол ABC пополам. Следовательно, угол ABM2 равен углу M2BC и составляет половину угла ABC, то есть ABM2 = M2BC = 1/2 ABC. Угол AQB, образованный прямой QP и стороной AB, равен 90° — 1/2 ABC, так как QP перпендикулярна BM2.
4. Найдем угол BPC в треугольнике BPC. Сумма углов треугольника равна 180°, поэтому угол BPC равен 180° — угол PBC — угол PCB. Подставим значения: угол PBC равен 90° — 1/2 ABC, а угол PCB равен 90° — 1/2 BCA. Тогда угол BPC = 180° — (90° — 1/2 ABC) — (90° — 1/2 BCA). Упростим выражение: угол BPC = 90° — 1/2 BAC.
5. Аналогично найдем угол CRA в треугольнике ARC. Сумма углов треугольника равна 180°, поэтому угол CRA равен 180° — угол CAR — угол ACR. Подставим значения: угол CAR равен 90° — 1/2 BAC, а угол ACR равен 90° — 1/2 BCA. Тогда угол CRA = 180° — (90° — 1/2 BAC) — (90° — 1/2 BCA). Упростим выражение: угол CRA = 90° — 1/2 ABC.
6. Найдем угол AQB в треугольнике AQB. Сумма углов треугольника равна 180°, поэтому угол AQB равен 180° — угол QAB — угол QBA. Подставим значения: угол QAB равен 90° — 1/2 BAC, а угол QBA равен 90° — 1/2 ABC. Тогда угол AQB = 180° — (90° — 1/2 BAC) — (90° — 1/2 ABC). Упростим выражение: угол AQB = 90° — 1/2 BCA.
7. Таким образом, мы видим, что все углы треугольников AQB, BPC, ARC равны:
Угол AQB = угол BPC = угол CRA = 90° — 1/2 BCA.
Угол QAB = угол PBC = угол CAR = 90° — 1/2 BAC.
Угол QBA = угол PCB = угол ACR = 90° — 1/2 ABC.
Следовательно, треугольники AQB, BPC, ARC подобны по равенству всех углов.
Ответ: Треугольники AQB, BPC, ARC подобны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!