
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 331 Атанасян — Подробные Ответы
Две стороны и угол одного треугольника равны каким-то двум сторонам и углу другого треугольника. Могут ли эти треугольники быть неравными?
Даны два треугольника ABC и A₁B₁C₁.
Пусть угол A равен углу C₁, стороны AB и A₁B₁, AC и A₁C₁ равны. В треугольнике ABC меньшая сторона BC лежит напротив меньшего угла A. В треугольнике A₁B₁C₁ угол B₁ равен углу A, но сторона A₁B₁ оказывается наименьшей, что возможно, если угол C₁ больше угла B₁. Это приводит к тому, что сторона B₁C₁ не равна стороне BC. Следовательно, треугольники могут быть неравными.
Даны два треугольника ABC и A₁B₁C₁. Условие задачи гласит, что две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника. Требуется выяснить, могут ли такие треугольники быть неравными.
Рассмотрим решение задачи:
1. Пусть угол A треугольника ABC равен углу C₁ треугольника A₁B₁C₁. При этом угол A является наименьшим углом в треугольнике ABC. Также по условию стороны AB и A₁B₁, AC и A₁C₁ равны.
2. В треугольнике ABC меньшая сторона BC лежит напротив меньшего угла A. Это следует из свойства треугольников: напротив меньшего угла всегда лежит меньшая сторона.
3. Теперь рассмотрим треугольник A₁B₁C₁. В этом треугольнике угол B₁ равен углу A треугольника ABC. Однако в треугольнике A₁B₁C₁ сторона A₁B₁ (равная стороне AB треугольника ABC) оказывается наименьшей стороной. Это возможно, если угол C₁ больше угла B₁.
4. Из этого следует, что сторона B₁C₁ треугольника A₁B₁C₁ не равна стороне BC треугольника ABC, так как в треугольнике A₁B₁C₁ другая сторона оказывается напротив меньшего угла.
5. Таким образом, треугольники ABC и A₁B₁C₁ не равны, несмотря на равенство двух сторон и одного угла.
Вывод: треугольники могут быть неравными, если в одном из них между двумя равными сторонами лежит больший или меньший угол, а в другом треугольнике этот угол находится напротив одной из данных сторон. Это приводит к различию в длинах соответствующих сторон, что делает треугольники неравными.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


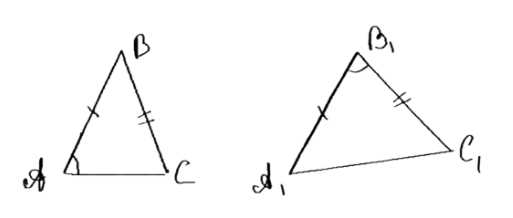

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!