
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 330 Атанасян — Подробные Ответы
Сторона и два угла одного треугольника равны какой-то стороне и каким-то двум углам другого. Могут ли эти треугольники быть неравными?
Дано два треугольника, у которых два угла равны и одна сторона равна.
Треугольники могут быть неравными, если одинаковая сторона лежит напротив разных углов. Например, в одном треугольнике сторона может быть напротив меньшего угла, а в другом — напротив большего. Это приводит к различию в форме треугольников, несмотря на совпадение двух углов и одной стороны.
Дано: два угла одного треугольника равны двум углам другого треугольника, а также одна из сторон одного треугольника равна соответствующей стороне другого. Требуется выяснить, могут ли такие треугольники быть неравными.
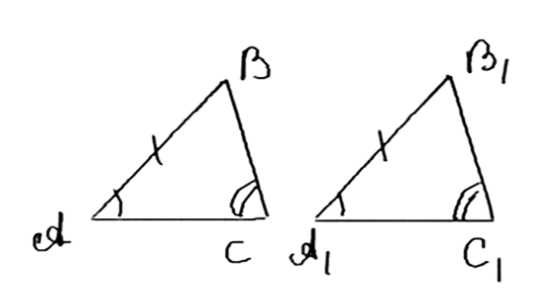
Пусть даны два треугольника ABC и A₁B₁C₁. Предположим, что угол A равен углу A₁, угол B равен углу B₁, а сторона AB равна стороне A₁B₁.
1. Так как в треугольниках сумма углов равна 180 градусам, то из равенства двух углов (угол A равен углу A₁ и угол B равен углу B₁) следует, что третий угол в треугольниках также равен. То есть угол C равен углу C₁.
2. Теперь рассмотрим треугольник ABC. Пусть AB — это сторона, равная A₁B₁. В треугольнике ABC угол C — наименьший (например, он меньше углов A и B). По теореме о соотношении сторон и углов в треугольнике, напротив меньшего угла лежит меньшая сторона. Следовательно, сторона BC будет меньше стороны AB.
3. В треугольнике A₁B₁C₁ ситуация может быть иной. Если сторона A₁B₁ равна стороне AB, но угол C₁ (равный углу C) прилегает к стороне A₁B₁, то расположение сторон относительно углов будет отличаться. Это означает, что сторона A₁C₁ может быть больше или меньше стороны BC в зависимости от того, как расположены углы и стороны.
4. Таким образом, хотя углы A и A₁, B и B₁, C и C₁ равны, а стороны AB и A₁B₁ равны, треугольники могут быть различными, если их стороны распределены относительно углов по-разному.
5. Примером такой ситуации может быть случай, когда один треугольник остроугольный, а другой тупоугольный. В остроугольном треугольнике сторона, равная данной, может быть напротив меньшего угла, тогда как в тупоугольном треугольнике эта же сторона может прилегать к большему углу. Это приводит к различию в форме треугольников.
Вывод: треугольники могут быть неравными, несмотря на равенство двух углов и одной стороны, если расположение углов и сторон относительно друг друга различается.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!