
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 329 Атанасян — Подробные Ответы
Докажите, что если угол, прилежащая к нему сторона и сумма двух других сторон одного треугольника соответственно равны углу, прилежащей к нему стороне и сумме двух других сторон другого треугольника, то такие треугольники равны.
Дано: угол A равен углу A₁, сторона AB равна стороне A₁B₁, сумма AC + BC равна A₁C₁ + B₁C₁. Требуется доказать равенство треугольников ABC и A₁B₁C₁.
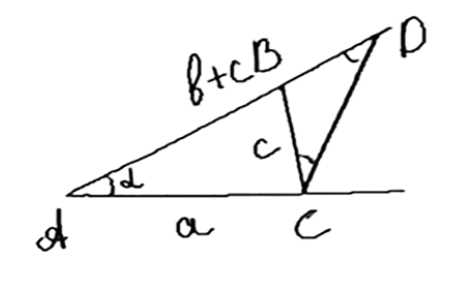
Рассмотрим треугольник ABC. По углу A и стороне AB треугольник строится однозначно, если задана сумма AC + BC. На луче, образующем угол A, откладывается точка D, такая что AD равно AC + BC. Точка C находится на пересечении серединного перпендикуляра к отрезку DB и прямой AD. Это определяет треугольник ABC однозначно.
Аналогично строится треугольник A₁B₁C₁ по тем же условиям. Поскольку данные одинаковы, треугольники совпадают. Следовательно, треугольники равны.
Дано: два треугольника ABC и A₁B₁C₁. Углы A и A₁ равны, стороны AB и A₁B₁ равны, а суммы сторон AC + BC и A₁C₁ + B₁C₁ также равны. Требуется доказать, что треугольники ABC и A₁B₁C₁ равны.
Рассмотрим доказательство:
1. Построим треугольник ABC, используя известные данные. Для этого выберем точку A и отложим от нее лучи, образующие угол A.
2. На одном из лучей отложим отрезок AB, равный заданной длине. Это возможно, так как длина AB известна.
3. На втором луче отложим отрезок AD, равный сумме двух сторон треугольника AC + BC. То есть AD = AC + CB.
4. Проведем серединный перпендикуляр к отрезку DB. Этот перпендикуляр пересечет прямую AD в некоторой точке C, так как точка C должна быть такой, чтобы выполнялось равенство AC + CB = AD.
5. Заметим, что так как AD = AC + CB и AD = AC + CD, то из равенства AC + CB = AC + CD следует, что CD = CB.
6. Таким образом, точка C однозначно определена, так как она лежит на пересечении серединного перпендикуляра к отрезку DB и прямой AD. Следовательно, треугольник ABC построен единственным образом.
7. Аналогично, треугольник A₁B₁C₁ строится по тем же самым данным: углу A₁, стороне A₁B₁ и сумме сторон A₁C₁ + B₁C₁.
8. Поскольку треугольники ABC и A₁B₁C₁ строятся по одинаковым данным (одинаковый угол, равная сторона и равная сумма двух других сторон), то они равны по первому признаку равенства треугольников.
Таким образом, доказано, что треугольники ABC и A₁B₁C₁ равны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!