Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 327 Атанасян — Подробные Ответы
Даны шесть точек. Известно, что прямая, проходящая через любые две точки, содержит по крайней мере ещё одну из данных точек. Докажите, что все эти точки лежат на одной
прямой.
Если шесть точек не лежат на одной прямой, их можно разделить на две группы, каждая из которых лежит на своей прямой. Рассмотрим прямую, проходящую через две точки из разных групп. По условию задачи такая прямая должна содержать хотя бы одну из оставшихся точек. Однако это невозможно, так как точки из одной группы не могут принадлежать прямой, проходящей через точки из другой группы. Это противоречие доказывает, что все шесть точек лежат на одной прямой.
Дано: шесть точек. Прямая, проходящая через любые две из этих точек, обязательно содержит хотя бы одну из оставшихся точек. Требуется доказать, что все шесть точек лежат на одной прямой.
Рассмотрим доказательство пошагово.
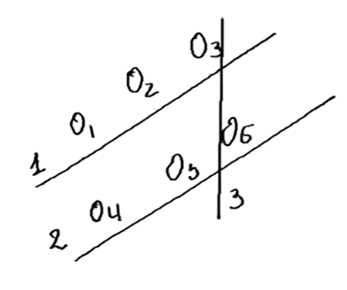
1. Предположим, что точки не лежат на одной прямой. Тогда их можно разбить на две группы, каждая из которых содержит три точки. Пусть точки O1, O2, O3 принадлежат одной прямой L1, а точки O4, O5, O6 принадлежат другой прямой L2.
2. Рассмотрим прямую, проходящую через две точки, принадлежащие разным прямым, например, через точки O1 и O4. По условию задачи, такая прямая должна содержать хотя бы одну из оставшихся точек. Однако это невозможно, так как точки O1, O2, O3 лежат на прямой L1, а точки O4, O5, O6 лежат на прямой L2. Следовательно, ни одна из точек O2, O3, O5, O6 не может одновременно принадлежать прямой, проходящей через точки O1 и O4.
3. Аналогично, если рассмотреть любую другую прямую, проходящую через две точки из разных групп, например, через точки O2 и O5, она также не может содержать третью точку из данных, так как точки внутри каждой группы принадлежат своей прямой.
4. Полученное противоречие доказывает, что разделение точек на две группы невозможно. Это означает, что все шесть точек должны лежать на одной прямой.
5. Таким образом, любая прямая, проходящая через две точки из данного множества, будет автоматически содержать третью точку, что соответствует условию задачи.
Доказательство завершено. Все шесть точек лежат на одной прямой.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.