Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
Основные особенности учебника:
- Структурированность материала:
- Учебник разделен на логические главы, каждая из которых охватывает определенную тему геометрии, что позволяет легко ориентироваться в материале.
- Доступность изложения:
- Язык и стиль написания адаптированы для школьников, что делает сложные концепции более понятными и доступными.
- Многообразие задач:
- В учебнике представлено множество задач различной сложности, что позволяет каждому ученику найти подходящие для себя упражнения и развивать свои навыки.
- Иллюстрации и схемы:
- Наглядные иллюстрации и схемы помогают лучше усвоить материал и визуализировать геометрические фигуры и их свойства.
- Практические примеры:
- Учебник включает практические примеры из реальной жизни, что делает изучение геометрии более увлекательным и актуальным.
- Поддержка для учителей:
- Включены методические рекомендации, которые помогут преподавателям эффективно использовать материал на уроках.
Заключение
Учебник Атанасяна по геометрии — это отличный инструмент для изучения предмета, который сочетает в себе доступность, разнообразие и практическую направленность. Он подходит как для самостоятельного изучения, так и для использования в классе, что делает его незаменимым помощником в образовательном процессе.
ГДЗ по Геометрии 7 класс Номер 326 Атанасян — Подробные Ответы
Даны шесть попарно пересекающихся прямых. Известно, что через точку пересечения любых двух прямых проходит по крайней мере ещё одна из данных прямых. Докажите, что все эти прямые проходят через одну точку.
Дано шесть прямых, каждая из которых попарно пересекается с другими, и через точку пересечения любых двух прямых проходит ещё одна из данных прямых.
Предположим, что не все шесть прямых пересекаются в одной точке. Тогда можно выделить хотя бы две точки пересечения, например O1 и O2, такие что O1 — точка пересечения трёх прямых, а O2 — точка пересечения других трёх. По условию задачи через каждую из этих точек должна проходить ещё хотя бы одна прямая из другой группы. Это приводит к необходимости существования третьей точки пересечения O3, через которую также должны проходить прямые из обеих групп. Однако это противоречит условию, так как через каждую точку пересечения любых двух прямых должна проходить ещё одна, а не несколько новых точек пересечения. Следовательно, все шесть прямых пересекаются в одной точке
Дано: шесть прямых, каждая из которых попарно пересекается с другими. Условие задачи гласит, что через точку пересечения любых двух прямых проходит по крайней мере ещё одна из данных прямых. Требуется доказать, что все шесть прямых пересекаются в одной точке.
Рассмотрим процесс доказательства по шагам:
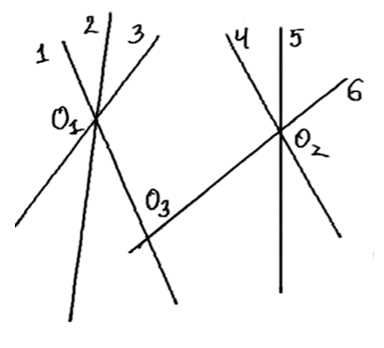
1. Начнем с того, что разобьем шесть прямых на две группы, каждая из которых состоит из трёх прямых. Пусть первая группа включает прямые 1, 2 и 3, а вторая группа — прямые 4, 5 и 6.
2. По условию задачи, прямые из первой группы пересекаются в одной точке, обозначим её O1. Это значит, что точка O1 является точкой пересечения прямых 1, 2 и 3. Аналогично, прямые из второй группы пересекаются в одной точке, обозначим её O2. Таким образом, точка O2 является точкой пересечения прямых 4, 5 и 6.
3. Теперь обратим внимание на условие задачи, которое утверждает, что через точку пересечения любых двух прямых должна проходить ещё одна из данных прямых. Это означает, что через точку O1 должна проходить хотя бы одна из прямых второй группы (например, прямая 4, 5 или 6). Аналогично, через точку O2 должна проходить хотя бы одна из прямых первой группы (например, прямая 1, 2 или 3).
4. Если через точку O1 проходит одна из прямых второй группы, а через точку O2 — одна из прямых первой группы, то возникает необходимость в существовании третьей точки пересечения, обозначим её O3. Точка O3 будет пересечением прямых из обеих групп.
5. Рассмотрим точку O3. По условию задачи, через точку пересечения любых двух прямых должна проходить ещё одна из данных прямых. Это возможно только в том случае, если все шесть прямых пересекаются в одной точке. Если бы все шесть прямых не пересекались в одной точке, то условие задачи нарушилось бы, так как не удалось бы обеспечить прохождение дополнительной прямой через точку пересечения.
6. Таким образом, предположение о том, что прямые могут пересекаться в разных точках, приводит к противоречию с условием задачи. Следовательно, все шесть прямых должны пересекаться в одной единственной точке.
Вывод: все шесть прямых пересекаются в одной точке. Доказательство завершено.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.