ГДЗ по Геометрии 7 класс Номер 320 Атанасян — Подробные Ответы

Постройте треугольник по стороне, высоте и медиане, проведённым к этой стороне.

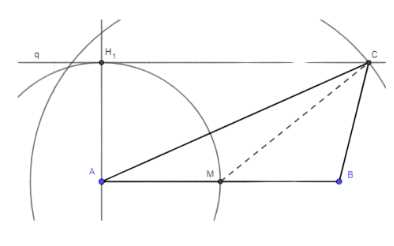
Найти середину отрезка AB и обозначить её точкой M. Построить перпендикуляр к AB в точке A и отложить на нём отрезок AH₁, равный высоте c. Провести прямую через точку H₁, перпендикулярную AH₁. Построить окружность с центром в точке M и радиусом, равным медиане a. На пересечении окружности и прямой отметить точку C. Соединить точки A, B и C.

Для построения треугольника ABC с заданными параметрами (медиана a, высота c) выполните следующие шаги:

1. Отрезок AB принимается как основание треугольника. На этом отрезке отложите его середину и обозначьте её точкой M. Таким образом, точка M делит отрезок AB пополам.

2. В точке A постройте перпендикуляр к отрезку AB. На этом перпендикуляре отложите отрезок AH₁, равный высоте c. Точка H₁ будет находиться на прямой, перпендикулярной AB, на расстоянии c от точки A.

3. Через точку H₁ проведите прямую q, которая будет перпендикулярна отрезку AH₁. Эта прямая q будет одной из опорных линий для дальнейших построений.

4. Постройте окружность с центром в точке M и радиусом, равным длине медианы a. Эта окружность пересечёт прямую q в двух точках.

5. Найдите точку пересечения окружности и прямой q, которая находится на стороне, противоположной отрезку AB. Обозначьте эту точку как C.

6. Соедините точки A, B и C. Получившийся треугольник ABC будет удовлетворять условиям задачи: медиана, проведённая к стороне AB, равна a, а высота, опущенная из вершины A, равна c.