
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 314 Атанасян — Подробные Ответы
Постройте прямоугольный треугольник по:
а) гипотенузе и острому углу;
б) катету и противолежащему углу;
в) гипотенузе и катету.
а) гипотенуза и острый угол:
1. Отложить отрезок AB, равный гипотенузе.
2. Построить угол, равный заданному острому углу.
3. Из точки B провести перпендикуляр к стороне угла.
4. Точка пересечения перпендикуляра и второй стороны угла — это точка C.
б) катет и противолежащий угол:
1. На стороне угла отметить произвольную точку C1.
2. Построить перпендикуляр из точки C1, отложив на нём отрезок C1B1, равный катету.
3. Построить перпендикуляр из точки B1, найти точку B.
4. Провести перпендикуляр из точки B, найти точку C.
в) гипотенуза и катет:
1. Построить отрезок BC, равный катету.
2. В точке C построить перпендикуляр.
3. Построить окружность с центром в точке B и радиусом, равным гипотенузе.
4. Точка пересечения окружности и перпендикуляра — это точка A.
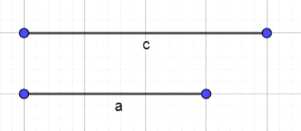
а) гипотенуза и острый угол:
1. Начертите прямую линию и отметьте на ней точку A.
2. Отложите отрезок AB, равный длине гипотенузы. Для этого с помощью линейки отметьте точку B так, чтобы расстояние AB соответствовало заданной длине.
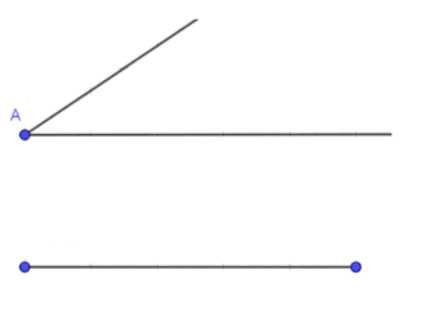
3. Постройте угол при вершине A, равный заданному острому углу. Для этого используйте транспортир, чтобы точно отложить угол.
4. Из точки B проведите перпендикуляр к стороне угла, используя угольник или циркуль.
5. Найдите точку пересечения перпендикуляра с другой стороной угла. Обозначьте эту точку как C.
6. Соедините точки A, B и C отрезками. Полученный треугольник является искомым.
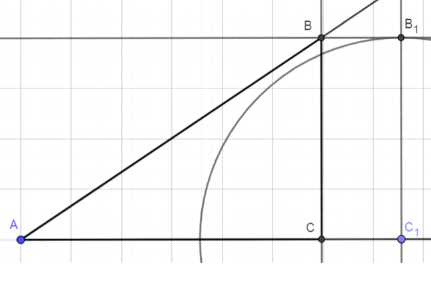
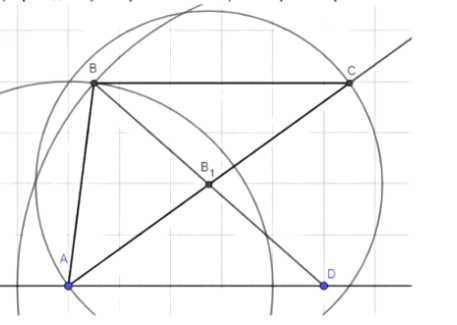
б) катет и противолежащий угол:
1. Начертите прямую линию и отметьте на ней произвольную точку C1.
2. Из точки C1 проведите перпендикуляр к прямой линии. На этом перпендикуляре отложите отрезок C1B1, равный длине катета. Для этого используйте линейку, чтобы точно измерить длину.
3. Из точки B1 постройте перпендикуляр к отрезку C1B1. Найдите точку пересечения этого перпендикуляра с прямой линией и обозначьте её как B.
4. Из точки B проведите перпендикуляр к линии. Найдите точку пересечения этого перпендикуляра с другой стороной угла и обозначьте её как C.
5. Соедините точки A, B и C отрезками. Полученный треугольник является искомым.
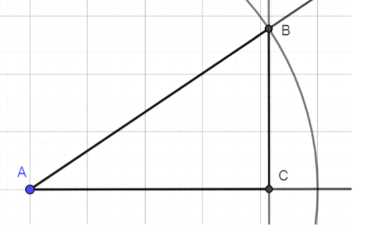
в) гипотенуза и катет:
1. Начертите прямую линию и отметьте на ней две точки B и C так, чтобы отрезок BC был равен длине катета. Для этого используйте линейку.
2. В точке C постройте перпендикуляр к линии BC. Для этого используйте угольник или циркуль.
3. Постройте окружность с центром в точке B и радиусом, равным длине гипотенузы. Для этого настройте циркуль на нужный радиус и проведите окружность.
4. Найдите точку пересечения окружности и перпендикуляра. Обозначьте эту точку как A.
5. Соедините точки A, B и C отрезками. Полученный треугольник является искомым.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!