
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 311 Атанасян — Подробные Ответы
Что представляет собой множество всех точек плоскости, каждая из которых равноудалена от двух данных пересекающихся прямых?
Дано две пересекающиеся прямые a и b. Требуется найти множество всех точек, равноудаленных от них. Решение: проводим биссектрисы углов, образованных прямыми a и b, обозначим их как c и d. Берем произвольную точку на одной из биссектрис, опускаем из нее перпендикуляры на прямые a и b. Рассматриваем два прямоугольных треугольника, которые образуются. Углы при вершине равны, так как это биссектриса, а одна из сторон общая. Треугольники равны по признаку равенства катета и прилежащего угла, значит длины перпендикуляров равны. Аналогично для второй биссектрисы. Таким образом, множество точек, равноудаленных от двух пересекающихся прямых, — это их биссектрисы.
Дано две пересекающиеся прямые a и b. Требуется найти множество всех точек, равноудаленных от этих прямых.
Рассмотрим пересечение прямых a и b. Обозначим точку пересечения как O. Пусть угол между прямыми a и b равен α. Проведем биссектрисы углов, образованных прямыми a и b. Обозначим их как c и d. Биссектрисы делят угол α и его смежный угол на две равные части.
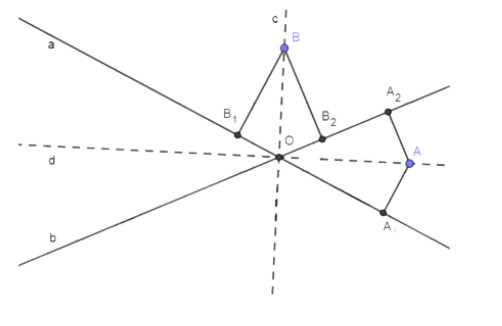
Возьмем произвольную точку A на одной из биссектрис, например, на d. Опустим из этой точки перпендикуляры AA₁ и AA₂ на прямые a и b соответственно. Рассмотрим два треугольника, которые образуются: треугольник AA₁O и треугольник AA₂O. Эти треугольники прямоугольные, так как AA₁ и AA₂ — перпендикуляры. Углы при вершине O равны, так как прямая d является биссектрисой угла между прямыми a и b. Сторона AO общая для обоих треугольников. Следовательно, треугольники равны по признаку равенства катета и прилежащего угла. Из равенства треугольников следует, что длины перпендикуляров AA₁ и AA₂ равны. Таким образом, любая точка на биссектрисе d равноудалена от прямых a и b.
Аналогично можно рассмотреть произвольную точку B на другой биссектрисе, то есть на c. Опустим из этой точки перпендикуляры BB₁ и BB₂ на прямые a и b. Аналогичное рассуждение показывает, что треугольники BB₁O и BB₂O равны, а значит, длины перпендикуляров BB₁ и BB₂ равны. Таким образом, любая точка на биссектрисе c также равноудалена от прямых a и b.
Следовательно, множество всех точек, равноудаленных от двух пересекающихся прямых a и b, образуют их биссектрисы c и d.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!