ГДЗ по Геометрии 7 класс Номер 308 Атанасян — Подробные Ответы

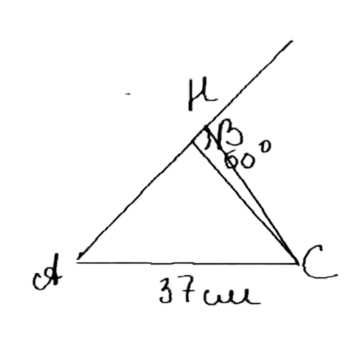
В равнобедренном треугольнике ABC с основанием АС, равным 37 см, внешний угол при вершине В равен 60°. Найдите расстояние от вершины С до прямой AB.

Дано: треугольник ABC равнобедренный, AB = BC, угол HBC = 60°, AC = 37 см. Нужно найти CH.

Решение:
1. Треугольник ABC равнобедренный, значит угол A равен углу BCA.
2. Угол ABC = 180° — 60° = 120° (как смежные углы).
3. Углы A и BCA равны: (180° — 120°) / 2 = 30°.
4. Рассмотрим прямоугольный треугольник CHC. Угол HCA = 30°, значит CH = AC / 2 = 37 / 2 = 18,5 см.

Ответ: CH = 18,5 см.

Дано: треугольник ABC равнобедренный, AB = BC, угол HBC = 60°, AC = 37 см. Требуется найти высоту CH, проведенную из вершины С на основание AB.

Решение:

1. Так как треугольник ABC равнобедренный (AB = BC), углы при основании равны. Обозначим угол A как α, тогда угол BCA также равен α.

2. Угол ABC является внешним углом для треугольника BHC. По свойству внешнего угла он равен сумме двух углов, не смежных с ним. Угол HBC равен 60° (по условию), следовательно, угол ABC = 180° — 60° = 120°.

3. В треугольнике ABC сумма всех углов равна 180°. Таким образом, угол при вершине A и угол при вершине C равны:
α + α + 120° = 180°,
2α = 60°,
α = 30°.

Следовательно, угол A = 30°, угол BCA = 30°.

4. Рассмотрим прямоугольный треугольник CHC. Угол HCA равен 30°, так как он является частью угла BCA. Из свойств прямоугольного треугольника с углом 30° известно, что катет, лежащий напротив угла 30°, равен половине гипотенузы.

5. В данном случае гипотенуза AC равна 37 см. Следовательно, высота CH равна:
CH = AC / 2 = 37 / 2 = 18,5 см.

Ответ: CH = 18,5 см.