ГДЗ по Геометрии 7 класс Номер 305 Атанасян — Подробные Ответы

Докажите, что сумма расстояний от любой точки, лежащей внутри треугольника, до его вершин меньше периметра треугольника.

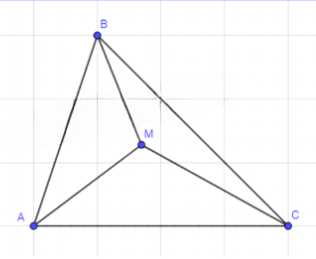
Дано: точка M лежит внутри треугольника ABC. Требуется доказать, что AM + BM + CM < AB + BC + AC.

Решение:

1. Рассмотрим треугольники ABM, BCM и CAM. Применим неравенство треугольника к каждой из них:
AM + BM > AB,
BM + CM > BC,
AM + CM > AC.

2. Складывая эти три неравенства, получаем:
(AM + BM) + (BM + CM) + (AM + CM) > AB + BC + AC.

3. Упростим левую часть:
2AM + 2BM + 2CM > AB + BC + AC.

4. Разделим обе части на 2:
AM + BM + CM < AB + BC + AC.

Таким образом, доказано, что сумма расстояний от точки M до вершин треугольника меньше его периметра.

Дано: Точка M лежит внутри треугольника ABC. Требуется доказать, что AM + BM + CM < AB + BC + AC.

Решение:

1. Рассмотрим треугольник ABM. Согласно неравенству треугольника, сумма длин двух сторон треугольника больше длины третьей стороны. Применим это правило для треугольника ABM:
AM + BM > AB.

2. Аналогично, рассмотрим треугольник BCM. По неравенству треугольника имеем:
BM + CM > BC.

3. Рассмотрим треугольник CAM. По неравенству треугольника получаем:
AM + CM > AC.

4. Складываем все три неравенства:
(AM + BM) + (BM + CM) + (AM + CM) > AB + BC + AC.

5. Упростим левую часть выражения. В сумме каждая из сторон AM, BM и CM встречается дважды:
2AM + 2BM + 2CM > AB + BC + AC.

6. Разделим обе части неравенства на 2:
AM + BM + CM < AB + BC + AC.

Таким образом, доказано, что сумма расстояний от точки M до вершин треугольника меньше периметра треугольника.