Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
Основные особенности учебника:
- Структурированность материала:
- Учебник разделен на логические главы, каждая из которых охватывает определенную тему геометрии, что позволяет легко ориентироваться в материале.
- Доступность изложения:
- Язык и стиль написания адаптированы для школьников, что делает сложные концепции более понятными и доступными.
- Многообразие задач:
- В учебнике представлено множество задач различной сложности, что позволяет каждому ученику найти подходящие для себя упражнения и развивать свои навыки.
- Иллюстрации и схемы:
- Наглядные иллюстрации и схемы помогают лучше усвоить материал и визуализировать геометрические фигуры и их свойства.
- Практические примеры:
- Учебник включает практические примеры из реальной жизни, что делает изучение геометрии более увлекательным и актуальным.
- Поддержка для учителей:
- Включены методические рекомендации, которые помогут преподавателям эффективно использовать материал на уроках.
Заключение
Учебник Атанасяна по геометрии — это отличный инструмент для изучения предмета, который сочетает в себе доступность, разнообразие и практическую направленность. Он подходит как для самостоятельного изучения, так и для использования в классе, что делает его незаменимым помощником в образовательном процессе.
ГДЗ по Геометрии 7 класс Номер 301 Атанасян — Подробные Ответы
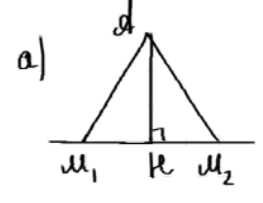
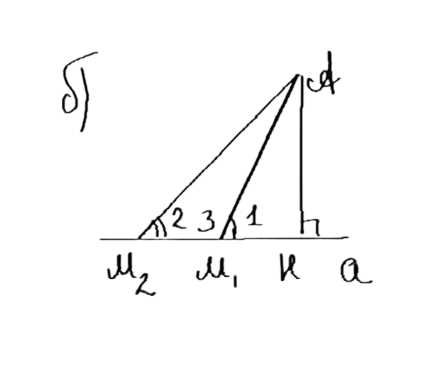
Из точки А к прямой а проведены перпендикуляр АН и наклонные АМ1 и АМ2. Докажите, что:
а) если HM1 = HM2, то AM1 = AM2;
б) если HM1 < HM2, то AM1 < АМ2.
а) Рассмотрим треугольники AM1H и AM2H. Они прямоугольные, так как AH перпендикулярно a. У них общий катет AH, углы при основании равны 90 градусов, и HM1 = HM2 по условию. Следовательно, треугольники равны, а значит, AM1 = AM2.
б) Рассмотрим треугольники AM1H и AM2H. Они прямоугольные, так как AH перпендикулярно a. Угол AM1H острый, угол AM2H острый, а угол между наклонными M1A и M2A тупой. Сторона AM1 лежит против острого угла, а сторона AM2 лежит против тупого угла. Так как сторона, лежащая против тупого угла, больше, то AM1 < AM2.
а) Рассмотрим треугольники AM1H и AM2H. Они оба прямоугольные, так как AH перпендикулярно прямой a. У этих треугольников общий катет AH. Углы при основании H равны 90 градусов, так как AH – это перпендикуляр. По условию задачи отрезки HM1 и HM2 равны, то есть HM1 = HM2. Таким образом, треугольники AM1H и AM2H равны по двум катетам. Из равенства треугольников следует, что их гипотенузы также равны, то есть AM1 = AM2. Задача доказана.
б) Рассмотрим треугольники AM1H и AM2H. Они оба прямоугольные, так как AH перпендикулярно прямой a. Угол AM1H острый, так как наклонная AM1 пересекает прямую a под углом. Аналогично, угол AM2H тоже острый, так как наклонная AM2 пересекает прямую a под углом. По условию задачи отрезок HM1 меньше отрезка HM2, то есть HM1 < HM2. Это означает, что точка M1 расположена ближе к основанию перпендикуляра H, чем точка M2.
В треугольнике AM1H гипотенуза AM1 лежит против острого угла при вершине M1. В треугольнике AM2H гипотенуза AM2 лежит против большего угла при вершине M2, так как HM2 больше HM1, а углы при основании наклонных зависят от длины перпендикуляра и наклонной. Следовательно, угол при вершине M2 больше, чем угол при вершине M1.
Из геометрических свойств треугольников известно, что сторона, лежащая против большего угла, всегда длиннее стороны, лежащей против меньшего угла. Таким образом, гипотенуза AM2 будет длиннее гипотенузы AM1, то есть AM1 < AM2. Задача доказана.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.