Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
Основные особенности учебника:
- Структурированность материала:
- Учебник разделен на логические главы, каждая из которых охватывает определенную тему геометрии, что позволяет легко ориентироваться в материале.
- Доступность изложения:
- Язык и стиль написания адаптированы для школьников, что делает сложные концепции более понятными и доступными.
- Многообразие задач:
- В учебнике представлено множество задач различной сложности, что позволяет каждому ученику найти подходящие для себя упражнения и развивать свои навыки.
- Иллюстрации и схемы:
- Наглядные иллюстрации и схемы помогают лучше усвоить материал и визуализировать геометрические фигуры и их свойства.
- Практические примеры:
- Учебник включает практические примеры из реальной жизни, что делает изучение геометрии более увлекательным и актуальным.
- Поддержка для учителей:
- Включены методические рекомендации, которые помогут преподавателям эффективно использовать материал на уроках.
Заключение
Учебник Атанасяна по геометрии — это отличный инструмент для изучения предмета, который сочетает в себе доступность, разнообразие и практическую направленность. Он подходит как для самостоятельного изучения, так и для использования в классе, что делает его незаменимым помощником в образовательном процессе.
ГДЗ по Геометрии 7 класс Номер 300 Атанасян — Подробные Ответы
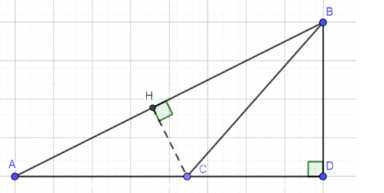
Докажите, что в тупоугольном треугольнике основание высоты, проведённой из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведённых из вершин острых углов, — на продолжениях сторон.
Высота из вершины тупого угла (C) пересекает сторону AB.
Высота из острого угла A пересекает продолжение стороны BC.
Высота из острого угла B пересекает продолжение стороны AC.
Объяснение:
- В тупоугольном треугольнике высота, проведённая из вершины тупого угла, всегда падает на противоположную сторону треугольника.
- Высоты, проведённые из вершин острых углов, пересекают продолжения противоположных сторон, так как угол между высотой и стороной оказывается внешним.
Рассмотрим тупоугольный треугольник ABC, где угол C является тупым (\[угол C > 90^\circ\]). Требуется доказать, что основание высоты, проведённой из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведённых из вершин острых углов, лежат на продолжениях сторон.
1. Проведём высоты из всех вершин треугольника. Пусть высота из вершины C пересекает сторону AB в точке D, высота из вершины A пересекает продолжение стороны BC в точке E, а высота из вершины B пересекает продолжение стороны AC в точке F.
2. Рассмотрим высоту CD, проведённую из тупого угла C. Высота по определению перпендикулярна стороне AB. Так как угол C тупой (\[угол C > 90^\circ\]), то стороны AC и BC расходятся, а сторона AB оказывается противоположной стороне угла C. Следовательно, основание высоты D лежит на стороне AB, так как перпендикуляр, опущенный из вершины C, пересекает саму сторону AB внутри треугольника.
3. Рассмотрим высоту AE, проведённую из вершины A. Высота по определению перпендикулярна стороне BC. Поскольку угол A острый (\[угол A < 90^\circ\]), вершина A находится внутри треугольника. Однако сторона BC продолжает уходить за пределы треугольника, так как угол C тупой. Поэтому перпендикуляр, опущенный из вершины A, пересекает продолжение стороны BC в точке E.
4. Аналогично, рассмотрим высоту BF, проведённую из вершины B. Высота по определению перпендикулярна стороне AC. Поскольку угол B острый (\[угол B < 90^\circ\]), вершина B также находится внутри треугольника. Однако сторона AC, подобно стороне BC, продолжает уходить за пределы треугольника. Поэтому перпендикуляр, опущенный из вершины B, пересекает продолжение стороны AC в точке F.
5. Таким образом, в тупоугольном треугольнике основание высоты, проведённой из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведённых из вершин острых углов, лежат на продолжениях сторон.
Доказательство завершено.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.