Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 296 Атанасян — Подробные Ответы
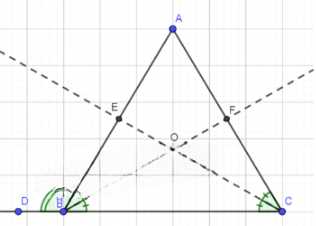
В равнобедренном треугольнике ABC биссектрисы равных углов В и С пересекаются в точке О. Докажите, что угол ВОС равен внешнему углу треугольника при вершине В.
- Рассмотрим треугольник ABC. Он равнобедренный, значит углы B и C равны.
- Биссектрисы углов B и C пересекаются в точке O. Это значит, что угол BOF равен углу COE, так как биссектрисы делят углы пополам.
- Угол LABD (внешний угол при вершине B) равен 180° — LABC, так как он смежный с внутренним углом треугольника.
- Рассмотрим треугольник BOC. Он равнобедренный, так как биссектрисы пересекаются в точке O, а стороны BO и CO равны.
- Угол BOC (угол при вершине O в треугольнике BOC) равен 180° — 2LB, так как сумма углов треугольника равна 180°, а треугольник равнобедренный.
- Внешний угол LABD равен 180° — LABC и совпадает с углом BOC, так как угол BOC равен 180° — 2LB, что доказывает равенство.
1. Рассмотрим треугольник ABC. По условию он равнобедренный, то есть AB = AC, а углы при основании B и C равны: ∠B = ∠C.
2. Биссектрисы углов B и C пересекаются в точке O. Это означает, что биссектрисы делят углы пополам: ∠ABF = ∠FBC и ∠ACE = ∠ECB.
3. Угол LABD – внешний угол при вершине B. Он равен разности 180° и внутреннего угла при вершине B, то есть:
LABD = 180° — ∠ABC.
4. Рассмотрим треугольник BOC. В этом треугольнике стороны BO и CO равны, так как они являются отрезками биссектрис углов B и C, пересекающихся в одной точке O. Следовательно, треугольник BOC равнобедренный.
5. В равнобедренном треугольнике углы при основании равны. Это означает, что в треугольнике BOC:
∠BOC = 180° — 2∠B,
так как сумма углов треугольника равна 180°, а два угла при основании равны.
6. Подставим выражение для внешнего угла LABD:
LABD = 180° — ∠ABC.
7. Так как треугольник равнобедренный и углы B и C равны, то:
∠ABC = ∠B.
8. Следовательно, внешний угол LABD можно записать как:
LABD = 180° — ∠B.
9. Угол BOC, найденный ранее, равен:
∠BOC = 180° — 2∠B.
10. Таким образом, угол BOC совпадает с внешним углом LABD, так как оба выражения равны:
LABD = ∠BOC.
Итак, доказано, что угол BOC равен внешнему углу треугольника при вершине B.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.