
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 295 Атанасян — Подробные Ответы
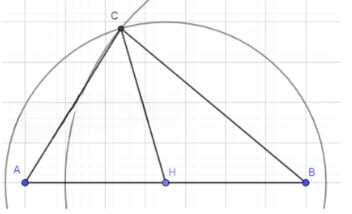
Постройте треугольник по двум сторонам и медиане, проведённой к одной из этих сторон.
Для построения треугольника по двум сторонам и медиане, проведённой к одной из сторон, выполните следующие шаги:
- Постройте основание AB, равное одной из заданных сторон.
- Найдите середину отрезка AB и обозначьте её точкой H.
- Постройте окружность с центром в точке H и радиусом, равным длине медианы.
- Постройте окружность с центром в точке A и радиусом, равным второй стороне треугольника.
- Найдите точки пересечения двух окружностей. Эти точки являются возможными положениями вершины C.
- Соедините точки A, B и C. Треугольник построен.
Для построения треугольника по двум сторонам и медиане, проведённой к одной из сторон, выполните следующие шаги:
1. Постройте отрезок AB, равный одной из заданных сторон треугольника. Это будет основание треугольника. Обозначьте его концы точками A и B.
2. Найдите середину отрезка AB. Для этого можно использовать циркуль: установите его в точку A, проведите дугу радиуса больше половины длины AB. Затем повторите это из точки B. Точки пересечения дуг соедините прямой, которая пересечёт AB в середине. Обозначьте середину как точку H.
3. Постройте окружность с центром в точке H и радиусом, равным длине медианы. Это можно сделать при помощи циркуля. Установите иглу циркуля в точку H, задайте радиус равным медиане и проведите окружность.
4. Постройте окружность с центром в точке A и радиусом, равным длине второй стороны треугольника. Для этого установите циркуль в точку A, задайте радиус равным длине стороны и проведите окружность.
5. Найдите точки пересечения двух окружностей. Эти точки будут возможными положениями вершины C треугольника. Обозначьте их как C1 и C2.
6. Соедините точки A, B и C1. Получившийся треугольник ABC1 является одним из возможных решений.
7. Соедините точки A, B и C2. Получившийся треугольник ABC2 является вторым возможным решением.
8. Проверьте, что построенные треугольники соответствуют исходным данным. Убедитесь, что длины сторон и медианы совпадают с заданными.
9. Если построение выполнено точно, оба треугольника являются решениями задачи.
10. Построение завершено. Убедитесь, что все шаги выполнены правильно, а чертёж соответствует условиям задачи.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!