
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 294 Атанасян — Подробные Ответы
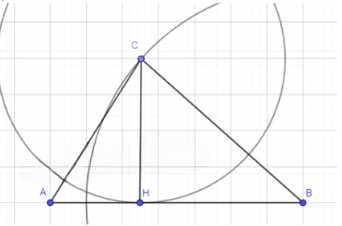
Постройте треугольник по двум сторонам и высоте, проведённой к одной из этих сторон.
1. Постройте отрезок AB, равный одной из сторон треугольника.
2. Восстановите из точки A перпендикуляр к отрезку AB.
3. На перпендикуляре отложите высоту AH, равную заданной.
4. Постройте окружность с центром в точке B и радиусом, равным второй стороне треугольника.
5. Найдите точку пересечения окружности с перпендикуляром. Эта точка будет вершиной C.
6. Соедините точки A, B и C. Треугольник построен.
1. Начнем с построения основания треугольника AB. Для этого отложите отрезок AB на плоскости, равный одной из заданных сторон треугольника. Обозначьте его концы точками A и B.
2. Из точки A восстановите перпендикуляр к отрезку AB. Для этого используйте линейку и транспортир или циркуль. Перпендикуляр должен быть проведен вверх или вниз от точки A, в зависимости от удобства.
3. На построенном перпендикуляре отложите высоту AH, равную заданной величине. Для этого установите циркуль на точку A, задайте радиус, равный высоте, и отметьте точку H на перпендикуляре.
4. Теперь из точки B постройте окружность с радиусом, равным второй стороне треугольника. Установите циркуль в точке B, задайте радиус равным длине второй стороны, и проведите окружность.
5. Найдите точку пересечения окружности с перпендикуляром AH. Это пересечение может быть в одной или двух точках. Выберите одну из точек пересечения и обозначьте ее как точку C.
6. Проверьте, чтобы длина отрезка AC соответствовала условиям задачи. Если длина совпадает, переходите к следующему шагу.
7. Соедините точки A, B и C отрезками. Получившийся треугольник ABC будет удовлетворять заданным условиям.
8. Убедитесь, что построенный треугольник соответствует всем исходным данным. Проверьте длины сторон AB, BC и AC, а также высоту AH.
9. Если построение выполнено точно, треугольник завершен.
10. Если при проверке обнаружены ошибки или несоответствия, повторите построение, начиная с первого шага, уточнив исходные данные и измерения.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!