
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 293 Атанасян — Подробные Ответы
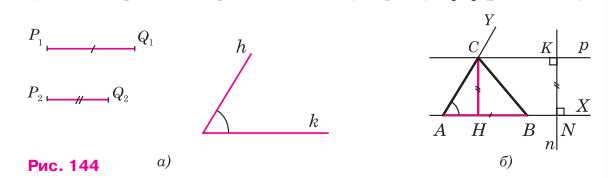
Даны отрезки P1Q1 и P2Q2 и угол hk. Требуется построить треугольник ABC, у которого одна из сторон, например AB, равна отрезку P1Q1, угол A равен углу hk, а высота CH, проведенная к стороне AB, равна отрезку P2Q2.
Для построения:
1. Построить угол XAY, равный углу hk.
2. На луче AX отложить отрезок AB, равный P1Q1.
3. Заметим, что расстояние от точки C до прямой AB должно равняться P2Q2. Множеством всех таких точек является прямая p, параллельная AB и находящаяся на расстоянии P2Q2 от AB.
4. Точка C — это пересечение прямой p и луча AY.
Таким образом, треугольник ABC удовлетворяет всем условиям задачи: AB = P1Q1, CH = P2Q2, угол A = hk.
Дан угол hk, отрезки P1Q1 и P2Q2. Построить угол XAY равный hk, отложить на луче AX отрезок AB равный P1Q1. Провести прямую p параллельную AB на расстоянии P2Q2. Точка C — пересечение прямой p и луча AY. Соединить точки A, B и C.
1. Начнем с построения угла hk. Для этого выберем произвольную точку A на плоскости и проведем два луча AX и AY так, чтобы угол между ними был равен заданному углу hk.
2. На луче AX отложим отрезок AB, равный длине отрезка P1Q1. Для этого с помощью циркуля измерим длину отрезка P1Q1, затем с центром в точке A и радиусом, равным этой длине, проведем дугу. Точка пересечения дуги с лучом AX будет точкой B.
3. Теперь определим местоположение точки C. Для этого нужно учесть, что высота CH, опущенная из точки C на сторону AB, должна быть равна длине отрезка P2Q2. Множеством всех точек, находящихся на фиксированном расстоянии от прямой AB, является две прямые, параллельные AB. Одна из них находится выше прямой AB, другая — ниже. Выберем одну из них в зависимости от расположения угла hk.
4. Построим параллельную прямую p, находящуюся на расстоянии P2Q2 от прямой AB. Для этого через точку A проведем перпендикуляр к прямой AB с помощью угольника или циркуля. Отложим на этом перпендикуляре расстояние, равное P2Q2, в обе стороны от прямой AB. Через полученные точки проведем прямую, параллельную AB.
5. Теперь найдем точку C. Она должна находиться на прямой p и на луче AY. Для этого определим точку пересечения прямой p и луча AY. Эта точка будет точкой C.
6. Соединим точки A, B и C отрезками. Получившийся треугольник ABC будет удовлетворять всем условиям задачи: сторона AB равна P1Q1, угол A равен hk, высота CH равна P2Q2.
7. Проверим построение. Измерим длину стороны AB, угол A и высоту CH. Убедимся, что они соответствуют заданным значениям. Если все выполнено корректно, построение завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!