
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 292 Атанасян — Подробные Ответы
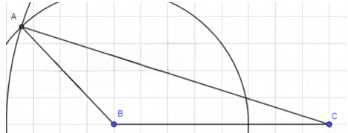
Даны отрезки P1Q1, P2Q2 и P3Q3. Постройте треугольник ABC так, чтобы:
а) AB = P1Q1, BC = P2Q2, CA = 2P3Q3;
б) AB = 2P1Q1, BC = P2Q2, CA = 3/2 P3Q3
1. Разделите отрезок P3Q3 на две равные части. Продолжите его на длину P3Q3 дважды.
2. Возьмите отрезок P2Q2 как основание треугольника и отметьте на его концах точки B и C.
3. Постройте окружность с центром в точке B радиусом, равным P1Q1 (для пункта а) или 2P1Q1 (для пункта б).
4. Постройте окружность с центром в точке C радиусом, равным 2P3Q3 (для пункта а) или 3/2 P3Q3 (для пункта б).
5. Точка пересечения окружностей будет точкой A. Соедините точки A, B и C отрезками.
6. Если окружности не пересекаются, задача не имеет решения, так как нарушается неравенство треугольника.
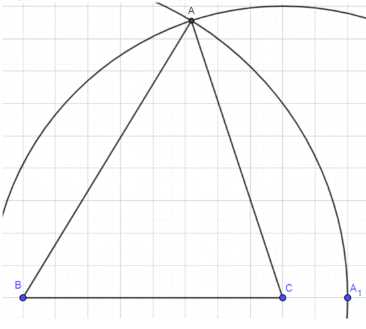
1. Для начала разделите отрезок P3Q3 на две равные части. Это можно сделать, используя циркуль: установите радиус, равный длине P3Q3, и отметьте точки пересечения дуг, построенных с концов отрезка. Соедините эти точки, чтобы получить середину отрезка.
2. Продолжите отрезок P3Q3 на его длину дважды. Для этого используйте ту же длину P3Q3 и отложите её дважды от конца отрезка в обоих направлениях.
3. Возьмите отрезок P2Q2 как основание треугольника. Отметьте на концах этого отрезка точки B и C. Это будет сторона BC треугольника.
4. Постройте окружность с центром в точке B. Радиус окружности равен P1Q1 для пункта а) или 2P1Q1 для пункта б). Для этого установите циркуль на точку B и отложите радиус, соответствующий указанной длине. Постройте полную окружность.
5. Постройте окружность с центром в точке C. Радиус окружности равен 2P3Q3 для пункта а) или 3/2 P3Q3 для пункта б). Аналогично предыдущему шагу, установите циркуль на точку C и постройте окружность с заданным радиусом.
6. Найдите точку пересечения двух окружностей, построенных на предыдущих шагах. Если окружности пересекаются в двух точках, выберите одну из них в зависимости от условий задачи. Эта точка будет точкой A.
7. Соедините точки A, B и C отрезками. Получившийся треугольник ABC будет удовлетворять условиям задачи.
8. Проверьте построение. Убедитесь, что длины сторон AB, BC и AC соответствуют указанным значениям (AB = P1Q1 или 2P1Q1, BC = P2Q2, AC = 2P3Q3 или 3/2 P3Q3). Если измерения совпадают, построение завершено.
9. Если окружности не пересекаются, это означает, что задача не имеет решения. Это может произойти, если одна из сторон треугольника больше или равна сумме двух других сторон, что нарушает неравенство треугольника.
10. Построение завершено, если все шаги выполнены корректно, и треугольник соответствует условиям задачи.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!