ГДЗ по Геометрии 7 класс Номер 291 Атанасян — Подробные Ответы

 Постройте равнобедренный треугольник:  

а) по боковой стороне и углу, противолежащему основанию;  

б) по основанию и углу при основании;  

в) по боковой стороне и углу при основании;  

г) по основанию и боковой стороне;  

д) по основанию и медиане, проведённой к основанию.

а) Построить луч, отложить на нем боковую сторону, затем на заданный угол построить второй луч и на нем отложить вторую боковую сторону. Соединить концы сторон.

б) Построить основание, затем из его концов провести лучи под заданными углами. На пересечении лучей отметить вершину треугольника и соединить точки.

в) Построить боковую сторону, затем от одного конца провести луч под заданным углом. На луче отложить вторую боковую сторону и соединить концы сторон.

г) Построить основание, найти его середину, восстановить перпендикуляр и отложить на нем высоту, равную боковой стороне. Соединить вершину с концами основания.

д) Построить основание, найти его середину, построить медиану, затем восстановить перпендикуляр и отложить на нем длину медианы. Соединить вершину с концами основания.

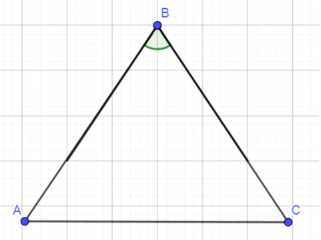
а) Построение по боковой стороне и углу, противолежащему основанию:

1. Отметьте точку 
   $A$ 

   $A$, которая будет вершиной треугольника.

2. Проведите луч 
   $AB$ 

   $AB$, равный длине боковой стороны.

3. В точке 
   $A$ 

   $A$ постройте угол, равный заданному углу, противолежащему основанию.

4. На втором луче угла отложите отрезок 
   $AC$ 

   $AC$, равный боковой стороне.

5. Соедините точки 
   $B$ 

   $B$ и  $C$ 

   $C$. Полученный треугольник  $ABC$ 

   $ABC$ будет равнобедренным.

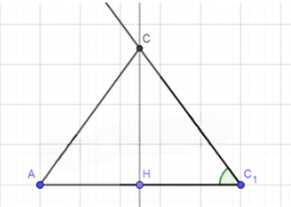
б) Построение по основанию и углу при основании:

1. Отметьте точки 
   $A$ 

   $A$ и  $B$ 

   $B$, которые будут концами основания треугольника.

2. Проведите луч из точки 
   $A$ 

   $A$, образуя угол, равный заданному углу при основании.

3. Аналогично, из точки 
   $B$ 

   $B$ проведите луч, также образуя угол, равный заданному.

4. На пересечении двух лучей отметьте точку 
   $C$ 

   $C$.

5. Соедините точки 
   $A$ 

   $A$,  $B$ 

   $B$ и  $C$ 

   $C$. Полученный треугольник  $ABC$ 

   $ABC$ будет равнобедренным.

в) Построение по боковой стороне и углу при основании:

1. Отметьте точку 
   $A$ 

   $A$, которая будет вершиной треугольника.

2. Проведите луч 
   $AB$ 

   $AB$, равный длине боковой стороны.

3. В точке 
   $A$ 

   $A$ постройте угол, равный заданному углу при основании.

4. На втором луче угла отложите отрезок 
   $AC$ 

   $AC$, равный боковой стороне.

5. Соедините точки 
   $B$ 

   $B$ и  $C$ 

   $C$. Полученный треугольник  $ABC$ 

   $ABC$ будет равнобедренным.

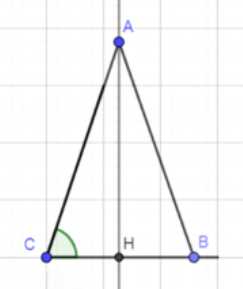
г) Построение по основанию и боковой стороне:

1. Отметьте точки 
   $A$ 

   $A$ и  $B$ 

   $B$, которые будут концами основания.

2. Найдите середину основания 
   $AB$ 

   $AB$ и отметьте её как точку  $M$ 

   $M$.

3. Постройте перпендикуляр из точки 
   $M$ 

   $M$ к основанию  $AB$ 

   $AB$.

4. На перпендикуляре отложите отрезок 
   $MC$ 

   $MC$, равный высоте треугольника, вычисленной из длины боковой стороны.

5. Соедините точки 
   $A$ 

   $A$,  $B$ 

   $B$ и  $C$ 

   $C$. Полученный треугольник  $ABC$ 

   $ABC$ будет равнобедренным.

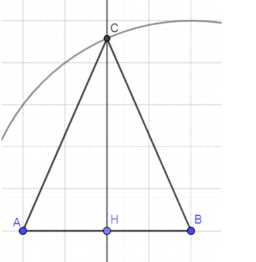
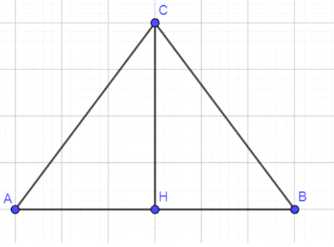
д) Построение по основанию и медиане, проведенной к основанию:

1. Отметьте точки 
   $A$ 

   $A$ и  $B$ 

   $B$, которые будут концами основания.

2. Найдите середину основания 
   $AB$ 

   $AB$ и отметьте её как точку  $M$ 

   $M$.

3. Проведите медиану 
   $CM$ 

   $CM$, равную заданной длине.

4. Постройте перпендикуляр из точки 
   $M$ 

   $M$ к основанию  $AB$ 

   $AB$.

5. На перпендикуляре отложите отрезок 
   $CM$ 

   $CM$, равный длине медианы.

6. Соедините точки 
   $A$ 

   $A$,  $B$ 

   $B$ и  $C$ 

   $C$. Полученный треугольник  $ABC$ 

   $ABC$ будет равнобедренным.