
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 286 Атанасян — Подробные Ответы
Постройте треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведённой из вершины этого угла.
Для построения треугольника по стороне, прилежащему к ней углу и биссектрисе, выполните следующие шаги:
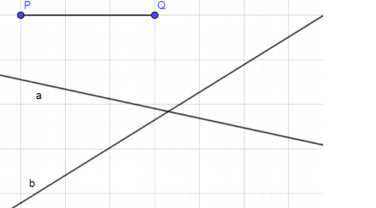
- Проведите отрезок AB, равный заданной стороне треугольника.
- В точке A постройте угол, равный заданному углу.
- На биссектрисе угла отложите отрезок AD, равный длине заданной биссектрисы.
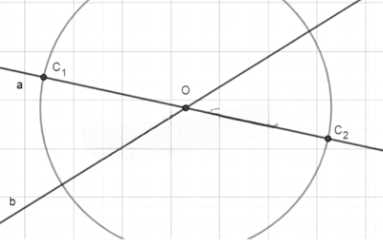
- Проведите окружность с центром в точке D и радиусом, равным расстоянию до точки B.
- Найдите точку пересечения окружности и прямой, проходящей через точку B под заданным углом. Это будет вершина C треугольника.
- Соедините точки A, B и C.
Для построения треугольника по стороне, прилежащему к ней углу и биссектрисе, выполните следующие действия:
1. Проведите отрезок AB, равный заданной стороне треугольника. Это будет основание треугольника.
2. В точке A постройте угол, равный заданному углу ∠BAC. Для этого используйте транспортир или подходящий инструмент.
3. На биссектрисе угла ∠BAC отложите отрезок AD, равный длине заданной биссектрисы. Для этого проведите прямую, делящую угол пополам, и отметьте на ней точку D так, чтобы длина AD равнялась заданной величине.
4. Постройте окружность с центром в точке D и радиусом, равным расстоянию от точки D до точки B. Это можно сделать с помощью циркуля.
5. Найдите точку пересечения окружности и прямой, проходящей через точку B под заданным углом. Это будет вершина C треугольника. Если существует два пересечения, выберите одно из них в зависимости от условий задачи.
6. Соедините точки A, B и C, чтобы получить треугольник ABC.
Детализация шагов:
1. Отрезок AB задает одну из сторон треугольника. Длина AB равна известной стороне треугольника.
2. Угол ∠BAC задает направление второй стороны треугольника AC. Биссектриса ∠BAC делит угол пополам, создавая равные углы между биссектрисой и сторонами треугольника.
3. Точка D находится на биссектрисе угла ∠BAC, и расстояние AD равно длине заданной биссектрисы. Это позволяет определить положение точки D.
4. Окружность с центром в точке D и радиусом DB используется для нахождения вершины C. Точка C должна находиться на окружности, так как расстояние от D до C равно расстоянию от D до B.
5. Пересечение окружности с прямой через B дает возможные положения точки C. Выбор конкретной точки зависит от дополнительных условий задачи.
6. Соединение точек A, B и C завершает построение треугольника.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!