
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 284 Атанасян — Подробные Ответы
Даны прямая a и отрезок AB. Постройте прямую р, параллельную прямой а, так, чтобы расстояние между прямыми a и р было равно AB.
Решение
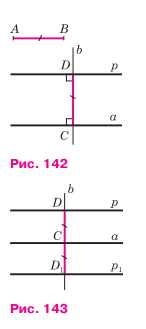
Отметим на прямой а какую-нибудь точку С и проведём через точку С прямую b, перпендикулярную к прямой а (рис. 142). Затем на одном из лучей прямой b, исходящих из точки С, отложим отрезок CD, равный отрезку AB. Через точку D проведём прямую р, перпендикулярную к прямой b. Прямая р — искомая (объясните почему). Как видно из построения, для любой данной прямой a и любого данного отрезка AB искомую прямую можно построить, причём задача имеет два решения (прямые р и р1 на рисунке 143).
Даны прямая a и отрезок AB. Отметьте на прямой a точку C. Проведите через точку C прямую b, перпендикулярную к прямой a. На прямой b отложите отрезок CD, равный отрезку AB. Через точку D проведите прямую p, параллельную прямой a. Прямая p — искомая, так как расстояние между прямыми a и p равно длине отрезка AB. Аналогично можно построить прямую p1 в противоположную сторону.
Рассмотрим задачу. Даны прямая a и отрезок AB. Требуется построить прямую p, параллельную прямой a, так, чтобы расстояние между прямыми a и p было равно длине отрезка AB.
Решение:
1. На прямой a выберем произвольную точку C. Это нужно для того, чтобы от этой точки строить перпендикуляр к прямой a.
2. Проведем через точку C прямую b, которая будет перпендикулярна прямой a. Для этого используем правило построения перпендикуляра к данной прямой через заданную точку. Прямая b пересекает прямую a в точке C и образует с ней угол 90 градусов.
3. На прямой b отложим отрезок CD, равный по длине отрезку AB. Для этого на одном из лучей прямой b, исходящих из точки C, отметим точку D так, чтобы длина отрезка CD равнялась длине отрезка AB. Это можно сделать с помощью циркуля, настроенного на длину отрезка AB.
4. Через точку D проведем прямую p, которая будет параллельна прямой a. Для этого строим прямую, которая проходит через точку D и не пересекается с прямой a, сохраняя одинаковое расстояние между ними.
5. Прямая p является искомой, так как по построению расстояние между прямыми a и p равно длине отрезка CD, а CD равно длине отрезка AB.
6. Аналогично, если на прямой b отложить отрезок CD в противоположную сторону от точки C, то получим точку D1. Через точку D1 можно провести прямую p1, которая также будет параллельна прямой a и находиться на расстоянии, равном длине отрезка AB.
Вывод: построение прямых p и p1 выполняется по заданным условиям, и обе эти прямые являются решениями задачи, так как они параллельны прямой a, а расстояние между каждой из них и прямой a равно длине отрезка AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!