
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 283 Атанасян — Подробные Ответы
Что представляет собой множество всех точек плоскости, находящихся на данном расстоянии от данной прямой?
Дано: прямые a и b параллельны, OX = OY.
Множество всех точек, находящихся на данном расстоянии от данной прямой, представляет собой две прямые, параллельные данной прямой и расположенные на заданном расстоянии по разные стороны от нее.
Рассмотрим треугольники ΔO₁O₂Y и ΔO₀O₁X. Они прямоугольные, так как OX = OY, углы ∠OYO₂ и ∠OXO₁ равны как накрест лежащие. По гипотенузе и острому углу треугольники равны. Следовательно, O₀O₁ = O₀O₂. Точка O равноудалена от прямых a и b, значит O лежит на прямой c, которая параллельна a и b. Таким образом, середины всех отрезков XY лежат на прямой c. Что и требовалось доказать.
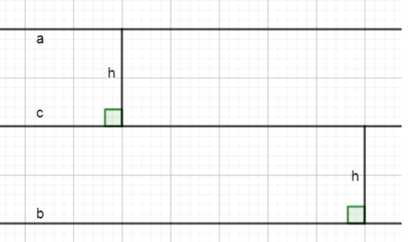
Рассмотрим условие задачи. Дана прямая c и требуется найти множество всех точек, находящихся на данном расстоянии h от этой прямой.
Решение:
1. Пусть прямая c задана на плоскости. Мы ищем такие точки, расстояние от которых до прямой c равно h. Расстояние от точки до прямой определяется как длина перпендикуляра, опущенного из точки на эту прямую.
2. Рассмотрим точку P, которая лежит на расстоянии h от прямой c. Если из этой точки провести перпендикуляр к прямой c, то длина этого перпендикуляра будет равна h. Точка P может находиться как выше прямой c, так и ниже нее, так как расстояние измеряется независимо от направления.
3. Таким образом, все точки, находящиеся на расстоянии h от прямой c, образуют две прямые, которые расположены параллельно прямой c. Эти прямые находятся на расстоянии h от прямой c: одна выше прямой c, другая ниже.
4. Эти две прямые параллельны прямой c, так как расстояние между параллельными прямыми в каждой точке одинаково и равно h. Это следует из определения параллельных прямых.
5. Следовательно, искомое множество всех точек, находящихся на расстоянии h от прямой c, представляет собой две прямые, параллельные прямой c и расположенные на расстоянии h по разные стороны от нее.
Вывод: множество всех точек, находящихся на данном расстоянии h от прямой c, состоит из двух прямых, которые параллельны прямой c и находятся на расстоянии h от нее.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!