ГДЗ по Геометрии 7 класс Номер 28 Атанасян — Подробные Ответы

Начертите прямую и отметьте на ней точки А и В. С помощью масштабной линейки отметьте точки С и D так, чтобы точка В была серединой отрезка АС, а точка D — серединой отрезка ВС.

• Начертите прямую линию и отметьте на ней точки A и B. Пусть AB = 4 единицы.
• Определите точку C так, чтобы точка B была серединой отрезка AC:
  • Расстояние от A до C должно быть вдвое больше расстояния от A до B.
  • Если AB = 4, то BC = 4, а AC = 8.
  • Точка C будет находиться на расстоянии 8 единиц от A.
• Определите точку D так, чтобы она была серединой отрезка BC:
  • Расстояние от B до C равно 4 единицам.
  • Точка D будет находиться на середине отрезка BC, то есть на расстоянии 2 единиц от B.
• Отметьте точки на чертеже:
  • A в начале прямой.
  • B на расстоянии 4 единиц от A.
  • C на расстоянии 8 единиц от A.
  • D на расстоянии 6 единиц от A (2 единицы от B).
• Подпишите точки A, B, C и D на чертеже.

• Начертите прямую линию и отметьте на ней точки A и B. Пусть расстояние между точками A и B равно 4 единицам (AB = 4). Это значение можно задать с помощью масштабной линейки.
• Определите расположение точки C таким образом, чтобы точка B была серединой отрезка AC:
  • Если точка B делит отрезок AC пополам, то длина отрезка AC должна быть вдвое больше длины отрезка AB.
  • Поскольку AB = 4, то длина отрезка AC будет равна 8 единицам (AC = 8).
  • Отметьте точку C на линии на расстоянии 8 единиц от точки A.
• Теперь определите точку D таким образом, чтобы она была серединой отрезка BC:
  • Длина отрезка BC равна 4 единицам (так как C находится на расстоянии 8 единиц от A, а B на расстоянии 4 единиц от A, следовательно, BC = 8 — 4 = 4).
  • Поскольку точка D делит отрезок BC пополам, она будет находиться на расстоянии 2 единиц от точки B.
  • Отметьте точку D на линии на расстоянии 6 единиц от точки A (так как 4 + 2 = 6).
• Проверьте правильность всех построений:
  • Точка B должна быть серединой отрезка AC. Это означает, что расстояние от A до B равно расстоянию от B до C (оба равны 4 единицам).
  • Точка D должна быть серединой отрезка BC. Это означает, что расстояние от B до D равно расстоянию от D до C (оба равны 2 единицам).
• Подпишите все точки на чертеже:
  • A — начало прямой.
  • B — на расстоянии 4 единиц от A.
  • C — на расстоянии 8 единиц от A.
  • D — на расстоянии 6 единиц от A.
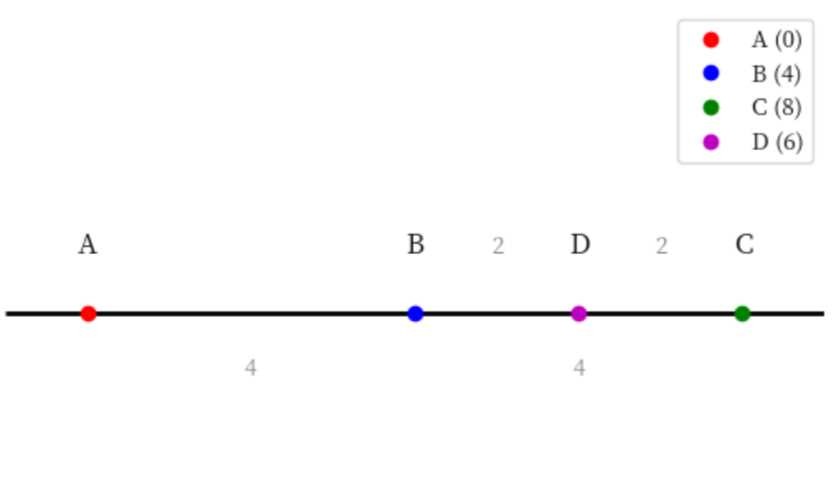
• Итоговые координаты точек:
  • A: 0
  • B: 4
  • D: 6
  • C: 8
• Постройте окончательный чертеж с указанными точками и расстояниями.