Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 279 Атанасян — Подробные Ответы
Докажите, что все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.
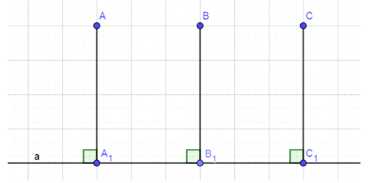
Дано: Прямая a, точки A, B, C равноудалены от прямой a. Требуется доказать, что точки A, B, C лежат на прямой b, параллельной a.
Решение:
1. Проведем через точку A прямую b, параллельную прямой a (по аксиоме параллельных прямых).
2. Все точки прямой b равноудалены от прямой a.
3. Предположим, что точки B и C не лежат на прямой b. Тогда расстояние от B или C до прямой a будет больше или меньше, чем расстояние от A до a, что противоречит условию задачи.
4. Следовательно, точки A, B, C лежат на одной прямой b, параллельной прямой a.
Доказано.
Дано: Прямая a, точки A, B, C равноудалены от прямой a. Требуется доказать, что точки A, B, C лежат на прямой b, параллельной прямой a.
Решение:
1. По условию задачи точки A, B, C равноудалены от прямой a. Это означает, что расстояния от каждой из точек A, B, C до прямой a равны между собой. Обозначим это расстояние как h.
2. Проведем через точку A прямую b, параллельную прямой a. Это возможно сделать по аксиоме параллельных прямых, согласно которой через любую точку пространства, не лежащую на данной прямой, можно провести единственную прямую, параллельную данной.
3. Все точки прямой b равноудалены от прямой a. Это свойство параллельных прямых, так как расстояние между параллельными прямыми в евклидовой геометрии постоянно.
4. Предположим, что точки B и C не лежат на прямой b. Тогда они не будут равноудалены от прямой a, так как любое отклонение от прямой b приведет к изменению расстояния от точек B и C до прямой a. Это противоречит условию задачи, где сказано, что все точки A, B, C равноудалены от прямой a.
5. Следовательно, точки B и C лежат на прямой b, так как только на этой прямой расстояние до прямой a остается равным h.
6. Таким образом, доказано, что все точки, равноудаленные от прямой a, лежат на прямой b, которая параллельна прямой a.
Доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.