
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 273 Атанасян — Подробные Ответы
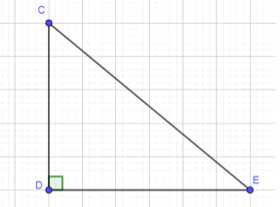
Сумма гипотенузы СЕ и катета CD прямоугольного треугольника CDE равна 31 см, а их разность равна 3 см. Найдите расстояние от вершины С до прямой DE.
Обозначим CD за x. Тогда CE можно выразить как x + 3, так как разность CE и CD равна 3 см. По условию, сумма CE и CD равна 31 см.
Составим уравнение:
x + (x + 3) = 31.
Решим уравнение:
2x + 3 = 31,
2x = 31 — 3,
2x = 28,
x = 28 / 2,
x = 14.
Таким образом, CD = 14 см. Ответ: 14 см.
Дано: прямоугольный треугольник CDE. По условию задачи известно, что сумма гипотенузы CE и катета CD равна 31 см, а их разность равна 3 см. Требуется найти длину катета CD.
Обозначим длину катета CD через x. Тогда длину гипотенузы CE можно выразить через x, так как разность CE и CD равна 3 см. Получаем:
CE = x + 3.
Также известно, что сумма CE и CD равна 31 см. Составим уравнение:
CD + CE = 31,
x + (x + 3) = 31.
Раскроем скобки и упростим уравнение:
x + x + 3 = 31,
2x + 3 = 31.
Теперь решим это уравнение. Выразим 2x:
2x = 31 — 3,
2x = 28.
Найдем x, разделив обе стороны на 2:
x = 28 / 2,
x = 14.
Таким образом, длина катета CD равна 14 см.
Проверим решение. Если CD = 14 см, то CE = CD + 3 = 14 + 3 = 17 см. Сумма CD и CE должна быть равна 31 см:
14 + 17 = 31.
Условие задачи выполнено, решение верное.
Ответ: CD = 14 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!