ГДЗ по Геометрии 7 класс Номер 272 Атанасян — Подробные Ответы

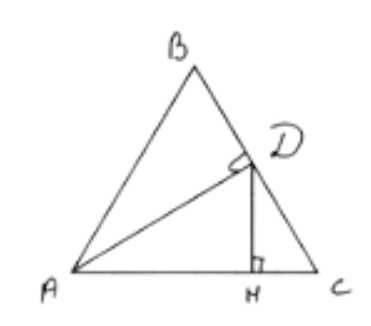
В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой АС равно 6 см. Найдите расстояние от вершины А до прямой ВС.

В равностороннем треугольнике ABC угол A равен 60°. Биссектриса AD является также высотой и медианой.

В прямоугольном треугольнике ADH, где DH = 6 см, угол HАD равен 30°. По свойству прямоугольного треугольника с углом 30° гипотенуза AD равна удвоенной длине противолежащего катета DH. Тогда AD = 2 * DH = 2 * 6 = 12 см. Ответ: 12 см.

Дан треугольник ABC, который является равносторонним. В таком треугольнике все стороны равны, а каждый угол равен 60°. Проведена биссектриса AD, которая в равностороннем треугольнике также является высотой и медианой. Это значит, что она делит угол A пополам, а сторону BC на две равные части. Точка H — основание перпендикуляра DH, проведенного из точки D на сторону AC. Известно, что DH = 6 см. Требуется найти длину отрезка AD.

Рассмотрим прямоугольный треугольник ADH. В этом треугольнике угол HАD равен 30°, так как угол A равен 60°, а биссектриса делит его пополам. Таким образом, угол HАD = 60° / 2 = 30°. Угол DHА равен 90°, так как DH — перпендикуляр к AC.

По свойству прямоугольного треугольника, в котором есть угол 30°, катет, лежащий напротив угла 30°, равен половине гипотенузы. В данном случае катет DH равен 6 см, и он лежит напротив угла 30°. Следовательно, гипотенуза AD равна удвоенной длине катета DH.

Вычислим длину AD:

AD = 2 * DH = 2 * 6 = 12 см.

Таким образом, длина AD равна 12 см. Проверка: в прямоугольном треугольнике с углом 30° это соотношение всегда выполняется. Ответ: AD = 12 см.