
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 270 Атанасян — Подробные Ответы
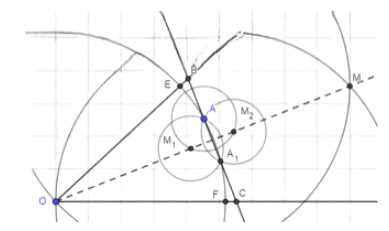
Внутри угла дана точка А. Постройте прямую, проходящую через точку А и отсекающую на сторонах угла равные отрезки.
1. Построить окружность с центром в точке O через точку A. Отметить точки E и F на пересечении окружности со сторонами угла.
2. Построить окружности с центрами в точках E и F радиусом EO = FO. Найти их точку пересечения M.
3. Провести луч OM, который является биссектрисой угла.
4. Построить окружность с центром в точке A произвольного радиуса, пересекающую луч OM в точках M1 и M2.
5. Построить окружности с центрами в точках M1 и M2 радиусом AM1 = AM2. Найти их точку пересечения A1.
6. Провести прямую через точки A и A1. Эта прямая отсекает равные отрезки на сторонах угла.
Для построения прямой, проходящей через точку A и отсекающей равные отрезки на сторонах угла, выполним следующие шаги:
1. Построим окружность с центром в точке O (вершина угла) и радиусом OA. Эта окружность пересечет стороны угла в точках E и F. Точки E и F — это точки пересечения окружности со сторонами угла.
2. Построим две окружности с одинаковым радиусом и центрами в точках E и F. Радиус этих окружностей выбираем равным расстоянию EO (или FO). Эти окружности пересекутся в двух точках, из которых выбираем точку M, находящуюся внутри угла.
3. Проведем луч OM. Этот луч является биссектрисой угла, так как он делит угол пополам. Теперь у нас есть биссектриса угла, проходящая через точку O и точку M.
4. Построим окружность с произвольным радиусом и центром в точке A. Эта окружность пересечет биссектрису OM в двух точках, которые обозначим как M1 и M2. Эти точки находятся на биссектрисе и равны по расстоянию от точки A.
5. Построим две окружности с центрами в точках M1 и M2 и радиусом, равным AM1 (или AM2). Эти окружности пересекутся в двух точках, из которых выбираем точку A1, находящуюся внутри угла.
6. Проведем прямую через точки A и A1. Эта прямая пересечет стороны угла в двух точках. Эти точки делят стороны угла на равные отрезки, так как построение выполнено симметрично относительно биссектрисы.
Таким образом, построенная прямая через точки A и A1 отсекает равные отрезки на сторонах угла.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!