ГДЗ по Геометрии 7 класс Номер 257 Атанасян — Подробные Ответы

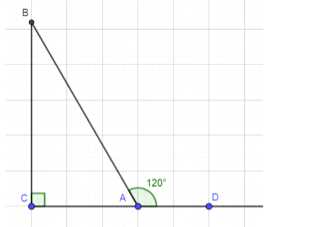
В прямоугольном треугольнике ABC c прямым углом С внешний угол при вершине А равен 120°, АС + AB = 18 см. Найдите АС и AB.

Дано: Внешний угол при вершине A равен 120°, значит угол BAC = 180° — 120° = 60°. Угол B = 90° — 60° = 30°. По свойству прямоугольного треугольника гипотенуза AB в 2 раза больше меньшего катета AC.

Обозначим AC = x, тогда AB = 2x. По условию: AC + AB = 18, значит x + 2x = 18. Решаем уравнение: 3x = 18, откуда x = 6.

AC = 6 см, AB = 2x = 12 см. Ответ: AC = 6 см, AB = 12 см.

Дано: Прямоугольный треугольник ABC, угол C = 90°, внешний угол при вершине A равен 120°. Сумма катета AC и гипотенузы AB равна 18 см. Требуется найти длины AC и AB.

Решение:

1. Внешний угол при вершине A равен 120°. Внутренний угол BAC треугольника можно найти как разность 180° и внешнего угла:
BAC = 180° — 120° = 60°.

2. В прямоугольном треугольнике сумма острых углов равна 90°. Следовательно, угол B равен:
B = 90° — BAC = 90° — 60° = 30°.

3. По свойству прямоугольного треугольника, катет, лежащий напротив угла в 30°, равен половине гипотенузы. В данном случае катет AC равен половине гипотенузы AB:
AC = AB / 2.

4. По условию задачи, сумма катета AC и гипотенузы AB равна 18 см. Запишем это уравнение:
AC + AB = 18.

5. Подставим вместо AC выражение AB / 2:
AB / 2 + AB = 18.

6. Приведем уравнение к общему знаменателю:
(AB + 2AB) / 2 = 18.

7. Упростим числитель:
3AB / 2 = 18.

8. Умножим обе стороны уравнения на 2, чтобы избавиться от знаменателя:
3AB = 36.

9. Разделим обе стороны уравнения на 3, чтобы найти AB:
AB = 36 / 3 = 12 см.

10. Найдем AC, используя соотношение AC = AB / 2:
AC = 12 / 2 = 6 см.

Ответ: AC = 6 см, AB = 12 см.