
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 252 Атанасян — Подробные Ответы
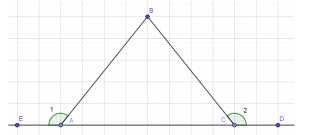
Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.
Для решения задачи:
- Пусть AB = BC (треугольник равнобедренный). Тогда: AC = 74 — (AB + BC) = 74 — 2AB. Проверяем неравенство треугольника: AB + BC > AC, AB + AC > BC, AC + BC > AB. Если AB = 16, то AC = 74 — 32 = 42. Проверка показывает, что 42 < 32 (неверно), значит AB ≠ 16.
- Пусть AC = 16. Тогда AB = BC = (74 — AC) / 2 = (74 — 16) / 2 = 29. Проверяем неравенство треугольника: AB + BC > AC, AB + AC > BC, AC + BC > AB. Все условия выполняются.
Ответ: AB = BC = 29 см, AC = 16 см.
Рассмотрим задачу. Нам дан треугольник, у которого два внешних угла при разных вершинах равны. Периметр треугольника равен 74 см, одна из сторон равна 16 см. Требуется найти две другие стороны треугольника. Решение будет следующим:
1. По условию задачи два внешних угла при разных вершинах равны. Это означает, что внутренние углы при этих вершинах тоже равны. Следовательно, треугольник является равнобедренным.
2. Пусть AB = BC (по признаку равнобедренного треугольника). Тогда третья сторона AC будет отличаться от AB и BC. Периметр треугольника равен 74 см, поэтому:
AB + BC + AC = 74.
3. Подставим AB = BC. Тогда:
AB + AB + AC = 74,
2AB + AC = 74,
AC = 74 — 2AB.
4. Рассмотрим первый случай: предположим, что AB = BC = 16 см. Тогда:
AC = 74 — 2 * 16 = 74 — 32 = 42 см.
5. Проверим неравенство треугольника для данного случая:
— AB + BC > AC: 16 + 16 > 42, 32 > 42 (неверно).
— Поскольку одно из условий неравенства треугольника не выполняется, данный случай невозможен.
6. Рассмотрим второй случай: предположим, что AC = 16 см. Тогда:
AB + BC = 74 — AC = 74 — 16 = 58,
AB = BC = 58 / 2 = 29 см.
7. Проверим неравенство треугольника для данного случая:
— AB + BC > AC: 29 + 29 > 16, 58 > 16 (верно),
— AB + AC > BC: 29 + 16 > 29, 45 > 29 (верно),
— AC + BC > AB: 16 + 29 > 29, 45 > 29 (верно).
8. Все условия неравенства треугольника выполняются. Следовательно, данный случай возможен.
Ответ: AB = BC = 29 см, AC = 16 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!