
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 247 Атанасян — Подробные Ответы
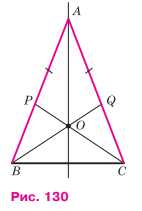
На рисунке 130 AB = АС, AP = AQ.
Докажите, что:
а) треугольник ВОС — равнобедренный;
б) прямая ОА проходит через середину основания ВС и перпендикулярна к нему.
а) Рассмотрим треугольники BPC и CQC. У них общая сторона BC, углы BPC и CQC равны, так как треугольник ABC равнобедренный, и отрезки PB и QC равны, так как AB = AC. Следовательно, треугольники BPC и CQC равны. Из этого следует, что BO = CO, поэтому треугольник BOC равнобедренный.
б) Рассмотрим треугольники BOA и COA. У них общая сторона AO, стороны BO и CO равны, так как треугольник BOC равнобедренный, и стороны AB и AC равны, так как треугольник ABC равнобедренный. Следовательно, треугольники BOA и COA равны. Отсюда угол BAO равен углу CAO, то есть AO является биссектрисой угла BAC. Поскольку треугольник ABC равнобедренный, биссектриса AO также является высотой и медианой. Следовательно, прямая AO проходит через середину стороны BC и перпендикулярна ей.
а) Докажем, что треугольник BOC равнобедренный.
1. Рассмотрим треугольники BPC и CQC. У этих треугольников общая сторона BC.
2. Углы ∠BPC и ∠CQC равны, так как треугольник ABC равнобедренный, и биссектрисы BO и CO делят угол ∠BAC пополам.
3. Отрезки PB и QC равны, так как AB = AC (по условию треугольник ABC равнобедренный), а отрезки PB и QC являются частями сторон AB и AC, отсеченными биссектрисами.
4. Следовательно, треугольники BPC и CQC равны по двум сторонам и углу между ними.
5. Из равенства треугольников BPC и CQC следует, что BO = CO.
6. Таким образом, треугольник BOC равнобедренный, так как у него две стороны равны.
б) Докажем, что прямая AO проходит через середину основания BC и перпендикулярна к нему.
1. Рассмотрим треугольники BOA и COA. У этих треугольников общая сторона AO.
2. Стороны BO и CO равны, так как треугольник BOC равнобедренный (доказано в пункте а).
3. Стороны AB и AC равны, так как треугольник ABC равнобедренный (по условию).
4. Следовательно, треугольники BOA и COA равны по трем сторонам.
5. Из равенства треугольников BOA и COA следует, что углы ∠BAO и ∠CAO равны. Это означает, что AO является биссектрисой угла ∠BAC.
6. Поскольку треугольник ABC равнобедренный, его биссектриса AO также является высотой и медианой (это свойство равнобедренного треугольника).
7. Из того, что AO является медианой, следует, что она проходит через середину стороны BC.
8. Из того, что AO является высотой, следует, что она перпендикулярна стороне BC.
9. Таким образом, доказано, что прямая AO проходит через середину стороны BC и перпендикулярна к ней.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!