ГДЗ по Геометрии 7 класс Номер 246 Атанасян — Подробные Ответы

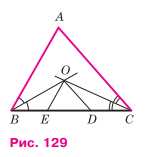
На рисунке 129 лучи ВО и СО — биссектрисы углов В и С треугольника ABC, ОE || AB, OD || AC. Докажите, что периметр треугольника EDO равен длине отрезка ВС.

Поскольку OE || AB и OD || AC, треугольник EDO подобен треугольнику ABC. Отрезок ED параллелен стороне BC и равен ей по длине. Периметр треугольника EDO равен сумме его сторон ED + EO + OD. Так как EO и OD пропорциональны сторонам AB и AC, а ED = BC, то периметр треугольника EDO равен длине отрезка BC.

Рассмотрим треугольник ABC, в котором проведены биссектрисы BO и CO, пересекающиеся в точке O. Через точку O проведены прямые, параллельные сторонам AB и AC, которые пересекают стороны треугольника в точках E и D соответственно. Нужно доказать, что периметр треугольника EDO равен длине стороны BC.

1. Поскольку OE параллельно AB, а OD параллельно AC, то треугольник EDO является гомотетичным треугольнику ABC. Центром гомотетии является точка O.

2. В результате гомотетии стороны треугольника EDO пропорциональны сторонам треугольника ABC. Отрезок ED параллелен стороне BC и равен ей по длине, так как ED — это часть прямой, параллельной BC.

3. Периметр треугольника EDO состоит из суммы длин его сторон: ED, EO и DO. Поскольку ED равно длине стороны BC, остается определить, как EO и DO связаны с другими сторонами треугольника ABC.

4. В силу гомотетии отрезки EO и DO пропорциональны сторонам AB и AC соответственно. Однако, поскольку ED = BC, периметр треугольника EDO можно выразить через длину стороны BC.

5. Таким образом, периметр треугольника EDO равен длине стороны BC, так как параллельность и пропорциональность сторон обеспечивают равенство всех частей треугольника EDO и проекции стороны BC.

Итак, доказано, что периметр треугольника EDO равен длине стороны BC.