
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 243 Атанасян — Подробные Ответы
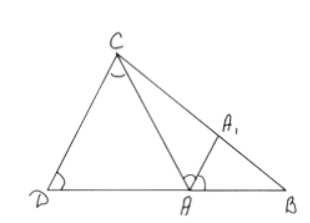
Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1 и пересекающая прямую AB в точке D. Докажите, что AC = AD.
Для решения задачи:
1. Рассмотрим, что AA1 — биссектриса угла A треугольника ABC, и CD || AA1.
2. Углы ∠A1AC и ∠ACD равны, так как они накрест лежащие при параллельных прямых CD и AA1 и секущей AC.
3. Углы ∠BAA1 и ∠ADC равны, так как они соответственные при параллельных прямых CD и AA1 и секущей AD.
4. Поскольку AA1 — биссектриса, то ∠A1AC = ∠BAA1. Следовательно, ∠ACD = ∠ADC.
5. Из равенства углов ∠ACD и ∠ADC следует, что треугольник ACD равнобедренный.
6. Таким образом, AC = AD, что и требовалось доказать.
Теперь создадим диаграмму, иллюстрирующую все случаи.
Дано: треугольник ABC, через вершину С проведена прямая CD, параллельная биссектрисе угла A (AA1), которая пересекает сторону AB в точке D. Требуется доказать, что AC = AD.
Решение:
1. Рассмотрим параллельные прямые CD и AA1, а также секущую AC. Поскольку CD || AA1, то углы ∠A1AC и ∠ACD равны как накрест лежащие. Обозначим их через α.
2. Рассмотрим те же параллельные прямые CD и AA1, но теперь секущую AD. Углы ∠BAA1 и ∠ADC равны как соответственные. Обозначим их через β.
3. Поскольку AA1 является биссектрисой угла A, то углы ∠A1AC и ∠BAA1 равны. Таким образом, α = β.
4. Из предыдущих шагов мы установили, что ∠ACD = ∠ADC. Следовательно, треугольник ACD равнобедренный, так как в равнобедренном треугольнике углы при основании равны.
5. В равнобедренном треугольнике ACD стороны AC и AD равны, так как напротив них лежат равные углы.
Вывод: AC = AD, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!