
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 238 Атанасян — Подробные Ответы
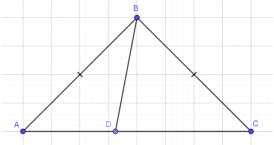
Докажите, что в равнобедренном треугольнике отрезок, соединяющий любую точку основания, отличную от вершины, с противоположной вершиной, меньше боковой стороны.
Дано: треугольник ABC равнобедренный (AB = AC), точка D лежит на основании BC. Необходимо доказать, что BD < AB.
1. Рассмотрим треугольники ABD и ABC. Треугольник ABC равнобедренный, поэтому AB = AC, а угол A меньше 90 градусов (углы в треугольнике не могут быть больше или равны 90 градусов одновременно).
2. Углы ADB и BDC являются смежными. Один из них тупой, другой острый, либо оба прямые.
3. Если угол ADB тупой, то он наибольший в треугольнике ABD. Следовательно, AB > BD.
4. Если угол BDC тупой, то он наибольший в треугольнике BDC. Следовательно, BC > BD, а так как AB = AC, то AB > BD.
5. Если углы ADB и BDC прямые, то треугольник ABD прямоугольный. В таком случае AB является гипотенузой, а BD катетом. Следовательно, AB > BD.
Таким образом, во всех случаях выполняется неравенство BD < AB. Что и требовалось доказать.
Дано: треугольник ABC равнобедренный (AB = AC), точка D лежит на основании BC. Требуется доказать, что BD < AB.
1. Рассмотрим треугольник ABC. Так как он равнобедренный, то AB = AC. Угол A при вершине меньше 90 градусов, так как в треугольнике сумма углов равна 180 градусам, а два угла одновременно не могут быть больше или равны 90 градусов.
2. Углы ADB и BDC являются смежными, так как точка D лежит на отрезке BC. Это означает, что сумма углов ADB и BDC равна 180 градусов. Следовательно, один из этих углов может быть тупым, а другой острым, либо оба угла могут быть прямыми.
3. Рассмотрим случай, когда угол ADB тупой. В треугольнике ABD угол ADB является наибольшим, так как тупой угол всегда больше острого. По свойству треугольника, сторона, лежащая напротив наибольшего угла, является наибольшей. Это значит, что AB > BD.
4. Рассмотрим случай, когда угол BDC тупой. В треугольнике BDC угол BDC является наибольшим. Это означает, что сторона BC больше стороны BD. Так как AB = AC (треугольник равнобедренный), а BC включает отрезок BD, то AB > BD.
5. Рассмотрим случай, когда углы ADB и BDC оба прямые. В таком случае треугольник ABD является прямоугольным, где угол ADB равен 90 градусов. В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. AB является гипотенузой, а BD — катетом. Следовательно, AB > BD.
6. Таким образом, во всех возможных случаях выполняется неравенство BD < AB.
Ответ: доказано, что BD < AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!