
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 222 Атанасян — Подробные Ответы
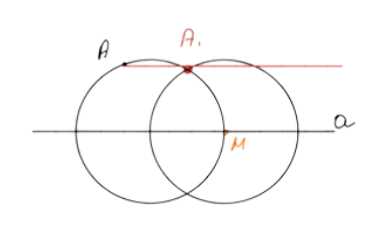
Даны прямая а и точка А, не лежащая на ней. С помощью циркуля и линейки через точку А проведите прямую, параллельную прямой а.
1. Установите циркуль на расстояние от точки A до прямой a.
2. Постройте окружность с центром в точке A. Она пересечет прямую a в точке O.
3. Постройте окружность с центром в точке O. Она пересечет прямую a в точках O1 и O2.
4. Постройте окружности с центрами в точках O1 и O2, используя радиус, равный радиусу первой окружности. Эти окружности пересекутся в точках A1 и A2.
5. Проведите прямую через точки A1 и A2. Эта прямая будет параллельна прямой a.
1. Установите циркуль таким образом, чтобы его радиус был равен расстоянию от точки A до прямой a. Это позволит построить окружность, касающуюся прямой a.
2. Постройте окружность с центром в точке A. Эта окружность пересечет прямую a в одной точке, которую обозначим как O.
3. Теперь переместите циркуль в точку O, не изменяя радиус. Постройте окружность с центром в точке O. Эта окружность пересечет прямую a в двух точках, которые обозначим как O1 и O2.
4. Установите циркуль в точку O1 и используйте радиус, равный радиусу первой окружности. Постройте окружность с центром в точке O1.
5. Переместите циркуль в точку O2, сохраняя тот же радиус, и постройте еще одну окружность с центром в точке O2.
6. Эти две окружности пересекутся в двух точках. Обозначьте эти точки как A1 и A2.
7. Проведите прямую через точки A1 и A2. Эта прямая будет параллельна заданной прямой a, так как она построена с использованием равных расстояний и симметрии, обеспеченной окружностями.
8. Убедитесь, что построенная прямая действительно параллельна прямой a, проверив, что расстояние между этими прямыми остается постоянным на всем их протяжении.
9. Построение завершено. Использование циркуля и линейки позволяет гарантировать точность и правильность построения.
10. Таким образом, прямая, проходящая через точки A1 и A2, является искомой прямой, параллельной прямой a.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!