ГДЗ по Геометрии 7 класс Номер 221 Атанасян — Подробные Ответы

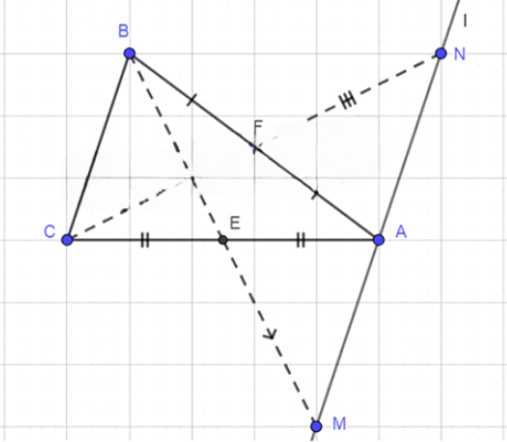
Даны треугольник ABC и точки М и N такие, что середина отрезка ВМ совпадает с серединой стороны АС, а середина отрезка CN — с серединой стороны AB. Докажите, что точки М, N и А лежат на одной прямой.

По условию середина отрезка BM совпадает с серединой стороны AC, а середина отрезка CN совпадает с серединой стороны AB. Это означает, что точки M и N определяются как такие, что отрезки BM и CN пересекают стороны AC и AB в их серединах. Таким образом, точки A, M и N лежат на одной прямой, так как средние линии треугольника, проведенные через вершину, пересекаются в одной точке.

Дано: треугольник ABC и точки M и N такие, что середина отрезка BM совпадает с серединой стороны AC, а середина отрезка CN совпадает с серединой стороны AB. Требуется доказать, что точки M, N и A лежат на одной прямой.

Рассмотрим решение.

1. Пусть D — середина стороны AC, а E — середина стороны AB. По условию, D — середина отрезка BM, а E — середина отрезка CN.

2. Рассмотрим точку D. Так как D — середина AC, то отрезок AD является медианой треугольника ABC. По условию, точка D также является серединой отрезка BM. Это означает, что точка M лежит на прямой AD, так как медиана делит отрезок BM пополам.

3. Аналогично, рассмотрим точку E. Так как E — середина AB, то отрезок AE является медианой треугольника ABC. По условию, точка E также является серединой отрезка CN. Это означает, что точка N лежит на прямой AE, так как медиана делит отрезок CN пополам.

4. Теперь у нас есть две медианы треугольника ABC: AD и AE. Из геометрии известно, что медианы треугольника пересекаются в одной точке, называемой центроидом треугольника. Это означает, что точки A, D и E лежат на одной прямой, а также точки M и N, так как они лежат на продолжениях соответствующих медиан.

5. Следовательно, точки A, M и N лежат на одной прямой, так как они связаны с медианами треугольника и их пересечением.

Доказательство завершено.