ГДЗ по Геометрии 7 класс Номер 220 Атанасян — Подробные Ответы

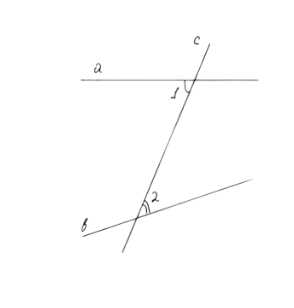
Докажите, что если при пересечении двух прямых a и b секущей накрест лежащие углы не равны, то прямые a и b пересекаются.

Если накрест лежащие углы, образованные прямыми a и b и секущей, не равны, то прямые a и b не параллельны, так как для параллельных прямых накрест лежащие углы равны. Если две прямые в одной плоскости не параллельны, они обязательно пересекаются. Следовательно, если накрест лежащие углы не равны, прямые a и b пересекаются.

Дано: две прямые a и b, пересеченные секущей. Накрест лежащие углы, образованные этими прямыми и секущей, не равны. Требуется доказать, что прямые a и b пересекаются.

Рассмотрим доказательство.

1. Накрест лежащие углы — это углы, которые находятся по разные стороны от секущей и на противоположных сторонах от пересекаемых прямых. Например, если секущая пересекает прямые a и b в точках, то один из накрест лежащих углов расположен в области выше прямой a, а другой — ниже прямой b.

2. Свойство параллельных прямых гласит, что если две прямые параллельны, то накрест лежащие углы, образованные этими прямыми и секущей, равны. Это следует из аксиом геометрии Евклида.

3. По условию задачи накрест лежащие углы не равны. Это означает, что прямые a и b не параллельны, так как равенство накрест лежащих углов — необходимое и достаточное условие параллельности двух прямых при наличии секущей.

4. Если две прямые лежат в одной плоскости и не параллельны, то они обязательно пересекаются. Это является следствием аксиом планиметрии, так как в одной плоскости две прямые либо параллельны, либо имеют единственную точку пересечения.

5. Таким образом, так как накрест лежащие углы не равны, прямые a и b не параллельны. А раз они не параллельны, то они пересекаются.

Доказательство завершено.