ГДЗ по Геометрии 7 класс Номер 218 Атанасян — Подробные Ответы

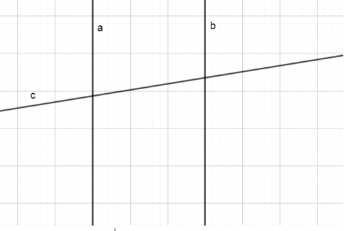
Прямые a и b параллельны прямой c. Докажите, что любая прямая, пересекающая прямую a, пересекает также и прямую b.

Дано:
a, b, c — прямые;
c пересекает a и c пересекает b.
Требуется доказать: a || b.

Доказательство:
1) Любая прямая, которая пересекает прямую a, также пересекает прямую b.
2) Две прямые не пересекаются только в том случае, если они параллельны. Следовательно, если прямая c не параллельна a, то она не будет параллельна и b.
3) Таким образом, прямая c не пересекает b только в случае, если она не пересекает a.
4) Из этого следует, что a || b, что и требовалось доказать.

Дано:
a, b, c — прямые;
c пересекает a и c пересекает b.
Требуется доказать, что a параллельна b.

Рассмотрим доказательство по шагам:

1. Прямая c пересекает как прямую a, так и прямую b, что означает, что она лежит в одной плоскости с ними. Это важно, так как для доказательства параллельности двух прямых необходимо, чтобы они находились в одной плоскости.

2. Если a и b не параллельны, то они должны пересекаться. Однако из условия задачи известно, что прямая c пересекает обе прямые, а значит, точка пересечения a и b, если бы она существовала, находилась бы на прямой c.

3. Если a и b пересекаются, то у них есть общая точка. Но в таком случае прямая c, пересекающая a и b, должна была бы пройти через эту общую точку, что противоречит ситуации, когда c пересекает a и b в разных точках.

4. Следовательно, прямые a и b не пересекаются.

5. Согласно определению параллельных прямых, если две прямые лежат в одной плоскости и не пересекаются, то они параллельны.

6. Таким образом, можно утверждать, что a параллельна b.

Доказательство завершено.