Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
Основные особенности учебника:
- Структурированность материала:
- Учебник разделен на логические главы, каждая из которых охватывает определенную тему геометрии, что позволяет легко ориентироваться в материале.
- Доступность изложения:
- Язык и стиль написания адаптированы для школьников, что делает сложные концепции более понятными и доступными.
- Многообразие задач:
- В учебнике представлено множество задач различной сложности, что позволяет каждому ученику найти подходящие для себя упражнения и развивать свои навыки.
- Иллюстрации и схемы:
- Наглядные иллюстрации и схемы помогают лучше усвоить материал и визуализировать геометрические фигуры и их свойства.
- Практические примеры:
- Учебник включает практические примеры из реальной жизни, что делает изучение геометрии более увлекательным и актуальным.
- Поддержка для учителей:
- Включены методические рекомендации, которые помогут преподавателям эффективно использовать материал на уроках.
Заключение
Учебник Атанасяна по геометрии — это отличный инструмент для изучения предмета, который сочетает в себе доступность, разнообразие и практическую направленность. Он подходит как для самостоятельного изучения, так и для использования в классе, что делает его незаменимым помощником в образовательном процессе.
ГДЗ по Геометрии 7 класс Номер 217 Атанасян — Подробные Ответы
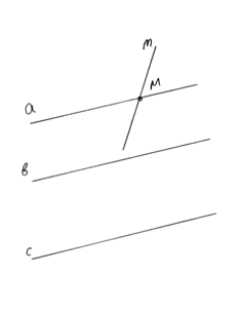
Прямые a и b параллельны прямой c. Докажите, что любая прямая, пересекающая прямую a, пересекает также и прямую b.
Прямые a и b параллельны третьей прямой c, следовательно, они параллельны между собой. Если прямая m пересекает одну из двух параллельных прямых, например a, то она обязательно пересечет и вторую прямую b, так как параллельные прямые находятся на одинаковом расстоянии друг от друга и имеют одинаковый наклон. Таким образом, любая прямая, пересекающая прямую a, пересечет и прямую b.
Рассмотрим задачу доказательства того, что любая прямая, пересекающая прямую a, пересечет также и прямую b, при условии, что прямые a и b параллельны третьей прямой c.
1. По условию задачи прямые a и b параллельны прямой c. Это означает, что все три прямые (a, b и c) имеют одинаковый наклон или находятся в одном направлении, не пересекая друг друга. Следовательно, прямые a и b также параллельны между собой.
2. Рассмотрим прямую m, которая пересекает прямую a. Прямая m, пересекающая одну из двух параллельных прямых, обязательно пересечет и вторую параллельную прямую. Это следует из свойства параллельных прямых: если две прямые параллельны, то любая секущая, пересекающая одну из них, пересечет и другую.
3. Для лучшего понимания рассмотрим геометрическую ситуацию на плоскости. Пусть прямая a имеет уравнение вида y = kx + b1, прямая b имеет уравнение y = kx + b2, а прямая c имеет уравнение y = kx + b3. Здесь k одинаково для всех трех прямых, поскольку они параллельны. Прямая m задается уравнением y = k1x + b, где наклон k1 отличается от k. Это гарантирует пересечение прямых.
4. Когда прямая m пересекает прямую a, это означает, что существует точка пересечения, координаты которой удовлетворяют уравнениям обеих прямых. Аналогично, поскольку прямая m имеет иной наклон, она обязательно пересечет и прямую b, так как b параллельна a и находится на фиксированном расстоянии от нее.
5. Таким образом, доказано, что любая прямая, пересекающая прямую a, пересечет также и прямую b.
Диаграмма, построенная ранее, иллюстрирует все случаи, где показаны параллельные прямые a, b, c и различные секущие прямые m и m’.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.