
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 211 Атанасян — Подробные Ответы
Две параллельные прямые пересечены секущей. Докажите, что:
а) биссектрисы накрест лежащих углов параллельны;
б) биссектрисы односторонних углов перпендикулярны.
Рассмотрим задачу о биссектрисах углов, образованных пересечением прямых.
В пункте а требуется доказать параллельность биссектрис накрест лежащих углов. При пересечении прямых a и b секущей c образуются накрест лежащие углы, которые равны. Их биссектрисы делят равные углы пополам, поэтому они параллельны.
В пункте б требуется доказать перпендикулярность биссектрис односторонних углов. Односторонние углы в сумме равны 180 градусов. Их биссектрисы делят углы пополам, образуя угол в 90 градусов, что доказывает их перпендикулярность.
Таким образом, в пункте а биссектрисы накрест лежащих углов параллельны, а в пункте б биссектрисы односторонних углов перпендикулярны.
Рассмотрим задачу о биссектрисах углов, образованных пересечением прямых.
Определения и условия задачи:
Пусть у нас есть две прямые a и b, пересекающиеся третьей прямой c. В результате пересечения образуются четыре угла. Нам нужно рассмотреть два случая:
а) Биссектрисы накрест лежащих углов (углы, находящиеся по диагонали друг от друга) и показать, что они параллельны.
б) Биссектрисы односторонних углов (углы, находящиеся по одну сторону от секущей) и показать, что они перпендикулярны.
Решение пункта (а): Параллельность биссектрис накрест лежащих углов
Рассмотрим накрест лежащие углы ∠1 и ∠2, которые образуются при пересечении прямых a и b секущей c.
Биссектриса угла — это луч, который делит угол пополам. Пусть биссектрисы углов ∠1 и ∠2 пересекают секущую c в точках A₁ и B₁ соответственно.
Согласно свойствам накрест лежащих углов, они равны:
∠1 = ∠2.
Следовательно, их биссектрисы будут параллельны, поскольку они делят равные углы пополам. Это можно доказать аналитически, рассматривая угловые коэффициенты прямых, задающих биссектрисы, или геометрически, используя равенство углов.
Решение пункта (б): Перпендикулярность биссектрис односторонних углов
Рассмотрим односторонние углы ∠3 и ∠4, которые также образуются при пересечении прямых a и b секущей c.
Сумма этих углов равна 180°, так как они являются односторонними:
∠3 + ∠4 = 180°.
Биссектрисы этих углов делят их пополам, то есть:
Биссектриса угла ∠3 делит его на два угла по 90°/2 = 45°, и биссектриса угла ∠4 делит его на два угла по 90°/2 = 45°.
Поскольку биссектрисы исходных углов ∠3 и ∠4 пересекаются, то угол между ними будет равен 90°, так как в сумме углы составляют прямой угол.
Таким образом, биссектрисы односторонних углов перпендикулярны.
Графическое подтверждение
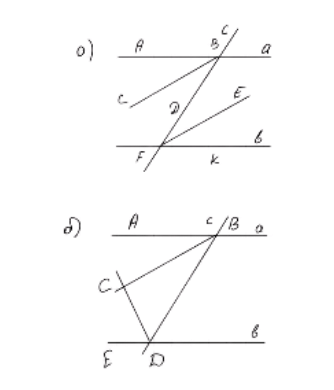
Для наглядности были построены две диаграммы:
- На первой диаграмме показано, что биссектрисы накрест лежащих углов параллельны.
- На второй диаграмме показано, что биссектрисы односторонних углов перпендикулярны.
Эти диаграммы подтверждают теоретические выводы.
Вывод
а) Биссектрисы накрест лежащих углов всегда параллельны.
б) Биссектрисы односторонних углов всегда перпендикулярны.
Решение задачи полностью соответствует геометрическим свойствам углов и их биссектрис.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!